Определитель матрицы
Определитель равен сумме произведений элементов какой-нибудь строки или столбца на их алгебраические дополнения, т.е.
, где i0 – фиксировано.
Выражение (*) называют разложением определителя D по элементам строки с номером i0.
Назначение сервиса. Данный сервис предназначен для нахождения определителя матрицы в онлайн режиме с оформлением всего хода решения в формате Word. Дополнительно создается шаблон решения в Excel.
Инструкция. Выберите размерность матрицы, нажмите Далее.
Вычислить определитель можно будет двумя способами: по определению и разложением по строке или столбцу. Если требуется найти определитель созданием нулей в одной из строк или столбцов, то можно использовать этот калькулятор.
Алгоритм нахождения определителя
- Для матриц порядка
n=2определитель вычисляется по формуле:Δ=a11*a22-a12*a21 - Для матриц порядка
n=3определитель вычисляется через алгебраические дополнения или методом Саррюса. - Матрица, имеющая размерность больше трех, раскладывается на алгебраические дополнения, для которых вычисляются свои определители (миноры). Например, определитель матрицы 4 порядка находится через разложение по строкам или столбцам (см. пример).
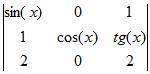
Используем прием разложения по первой строке.
Δ = sin(x)×[cos(x)×2 – 0×tg(x)] + 1×[1×0-2×cos(x)] = 2sin(x)cos(x)-2cos(x) = sin(2x)-2cos(x)
Оптимальный план вычисления определителя через алгебраические дополнения
При расчете определителя с помощью алгебраических дополнений для матриц размерностью n>4, чтобы не делать избыточные вычисления, можно предварительно находить индекс строки или столбца, в котором присутствуют максимальное количество нулей.Например для матрицы:
| A = |
|
| Δ1,3 = |
|
∆1,3 = 2*(1*(-1)-0*2)-0+(-2)*(0*2-1*1) = 0
Определитель:
∆ = (-1)1+3*(-2)*0 = -2*0 = 0
Методы вычислений определителей
Нахождение определителя через алгебраические дополнения является распространенным методом. Его упрощенным вариантом является вычисление определителя правилом Саррюса. Однако при большой размерности матрицы, используют следующие методы:- вычисление определителя методом понижения порядка
- вычисление определителя методом Гаусса (через приведение матрицы к треугольному виду).
- вычисление определителя методом декомпозиции.
В Excel для расчета определителя используется функция
=МОПРЕД(диапазон ячеек).
Прикладное использование определителей
Вычисляют определители, как правило, для конкретной системы, заданной в виде квадратной матрицы. Рассмотрим некоторые виды задач на нахождение определителя матрицы.- Решение СЛАУ. Если определитель системы не равен нулю (Δ ≠ 0), система имеет решение.
- При вычислении ранга матрицы также требуется наличие минора (текущего определителя для i-ой строки и j-го столбца), не равного нулю.
- Алгоритм нахождения обратной матрицы включает расчет определителя: если определитель равен нулю, обратной матрицы не существует.
- Определитель используется при вычислении площади треугольника:
.
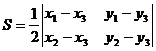- Значение определителя служить оценкой при максимизации удельного показателя перевозок.
- По знаку определителя устанавливают вид функции (выпуклая или вогнутая) при расчете матрицы Гессе.
- Отношение определителей корреляционных матриц позволяет находить множественный коэффициент корреляции и коэффициент детерминации.
|
Δ = 1(a*(-2)-0*1) -1(3*(-2)-1*1) + 2(3*0-1*a) = -2a+7-2a = -4a+7 = 0. Откуда a=7/4
Пример. Найти определитель матрицы:
| A = |
|
Найдем определитель, использовав разложение по столбцам (по первому столбцу):
Минор для (1,1): Вычеркиваем из матрицы первую строку и первый столбец.
| 1 | 0 | -2 |
| 3 | 2 | 1 |
| 1 | 2 | -2 |
Получаем:
| ∆ 1,1 = |
|
Найдем определитель для этого минора.
∆1,1 = (2 • (-2)-2 • 1) = -6.
Определим минор для (2,1): для этого вычеркиваем из матрицы вторую строку и первый столбец.
| 1 | 0 | -2 |
| 3 | 2 | 1 |
| 1 | 2 | -2 |
| ∆ 2,1 = |
|
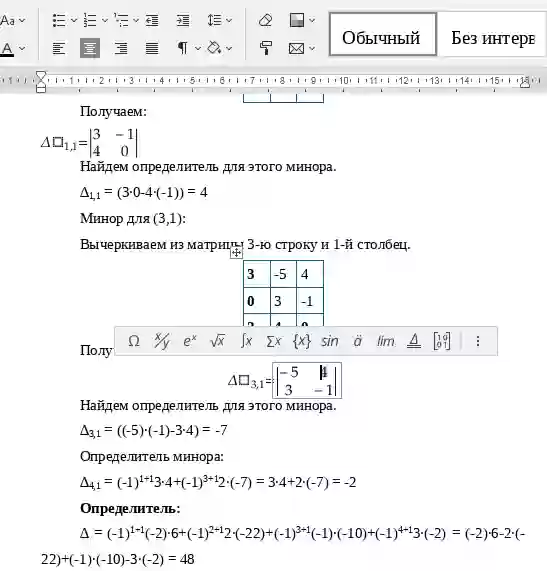
∆2,1 = (0 • (-2)-2 • (-2)) = 4. Минор для (3,1): Вычеркиваем из матрицы 3-ю строку и 1-й столбец.
| 1 | 0 | -2 |
| 3 | 2 | 1 |
| 1 | 2 | -2 |
Получаем:
| ∆ 3,1 = |
|
Найдем определитель для этого минора.
∆3,1 = (0 • 1-2 • (-2)) = 4
Главный определитель равен:
∆ = (1 • (-6)-3 • 4+1 • 4) = -14
Найдем определитель, использовав разложение по строкам (по первой строке):
Минор для (1,1): Вычеркиваем из матрицы первую строку и первый столбец.
| 1 | 0 | -2 |
| 3 | 2 | 1 |
| 1 | 2 | -2 |
Получаем:
| ∆ 1,1 = |
|
Найдем определитель для этого минора.
∆1,1 = (2 • (-2)-2 • 1) = -6. Минор для (1,2): Вычеркиваем из матрицы 1-ю строку и 2-й столбец.
| 1 | 0 | -2 |
| 3 | 2 | 1 |
| 1 | 2 | -2 |
| ∆ 2,1 = |
|
∆1,2 = (3 • (-2)-1 • 1) = -7. И чтобы найти минор для (1,3) вычеркиваем из матрицы первую строку и третий столбец.
| 1 | 0 | -2 |
| 3 | 2 | 1 |
| 1 | 2 | -2 |
Получаем:
| ∆ 3,1 = |
|
∆1,3 = (3 • 2-1 • 2) = 4
Находим главный определитель:
∆ = (1 • (-6)-0 • (-7)+(-2 • 4)) = -14
