Эллипс
Эллипс – геометрическое место точек, сумма расстояний от каждой из которых до двух данных точек F1,F2 (фокусы) есть величина постоянная, равная 2a.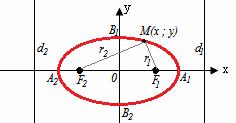
Элементы эллипса:
A1A2=2a - большая ось
B1B2=2b - большая ось
A1 ,A2 , B1 ,B2 , - вершины
F1(c ; 0), F2(-c ; 0) - фокусы
F1F2=2c - фокальное расстояние
c2=a2-b2
- эксцентриситет. Эксцентриситет эллипса можно рассматривать, как меру его «вытянутости»: чем больше эксцентриситет, тем меньше отношение 
r1=a-εx, r2= a+εx - фокальные радиусы
- директрисы
Каноническое уравнение эллипса (координатные оси совпадают с осями эллипса):
Параметрические уравнения:
Построение графика эллипса
Каждая новая функция вводится с новой строки. Для добавления точки с координатами (x,y) достаточно указать, например, A=(sqrt(2),3.9).Чтобы настроить вид координатной сетки (пределы по осям и стрелки) используйте
.
Эллипс также можно построить по его элементам (параметры a, b; эксцентриситет и координаты фокусов).
Построение графика эллипса по его элементам
Возможны два вариант построения графика эллипса:
- Заданы параметры a и b.
- Заданы параметры ε и фокус c (координаты F1, F2).
Пределы по OX:...
Пределы по OY:...
см. также Кривые второго порядка (Эллипс, Окружность, Гипербола, Парабола).
Приведение кривой второго порядка к каноническому виду.
.
Множество точек на плоскости (составить уравнение множества точек на плоскости, отношение расстояний которых от точки A(1;-2) и от прямой x=1 равно 1/2).
Приведение кривой второго порядка к каноническому виду.
.
Множество точек на плоскости (составить уравнение множества точек на плоскости, отношение расстояний которых от точки A(1;-2) и от прямой x=1 равно 1/2).
