Инструкция. Заполните коэффициенты при соответствующих переменных и нажмите кнопку Решение.
Например, для уравнения 1/2x2 + 5xy + 10y2 - 2/3x + y - 11 = 0, необходимо будет ввести коэффициенты: 1/2, 5, 10, -2/3, 1, -11. Корень числа вводится как sqrt. например, sqrt(2).
Если уравнение задано в виде 4y=-6-sqrt(4x-x2), то предварительно его необходимо преобразовать (см. примеры ниже).
Пример №1. Привести уравнение второго порядка к каноническому виду с помощью поворота и параллельного переноса осей координат. Построить кривую.
Пример №2. Выполнив последовательно преобразования координат: поворот, а затем параллельный перенос координатных осей, преобразовать к каноническому виду уравнение кривой второго порядка и построить ее в исходной системе координат, а также найти параметры кривой.
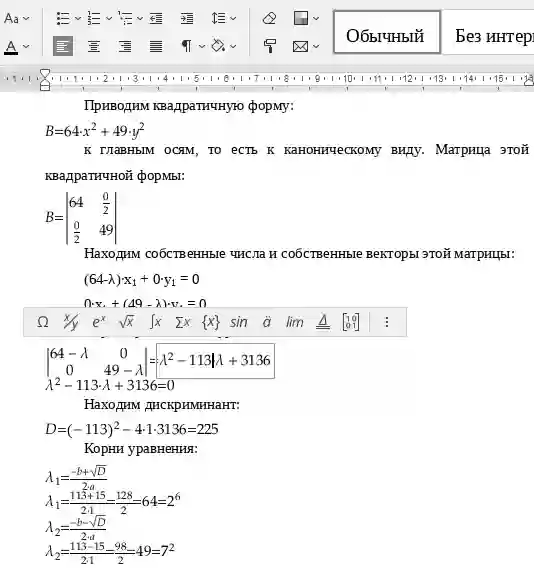
Приведение кривой второго порядка к каноническому виду
Уравнение второго порядка вида a11x2 + 2a12xy + a22y2 + 2a01x + 2a02y + a00 = 0 определяет на плоскости кривую.Канонический вид кривой второго порядка: λ1x2 + λ2y2, причем:
а) если λ1>0; λ2>0 – эллипс, в частности, при λ1=λ2 это окружность;
б) если λ1>0, λ2<0 (λ1<0, λ2>0) имеем гиперболу;
в) если λ1=0 либо λ2=0, то кривая является параболой.
Алгоритм перехода кривой второго порядка к каноническому виду
1. Переход к системе координат с осями x2=0, y2=0.


Пример №1. 4y=-6-sqrt(4x-x2)
sqrt(4x-x2) = -(4y+6)
Возведем в квадрат
4x-x2 = (4y+6)2
Раскрывая скобки, получаем:
16y2+48y + 36 +x2-4x = 0
Далее решается калькулятором. Если самостоятельно решать, то получим:
4x-x2 = (4y+6)2
-(x2 - 4x) = 2(y+3/2)2
-(x2 - 4x + 4) = (y+3/2)2
-(x - 2) 2 = (y+3/2)2
(y+3/2)2 + (x - 2)2 = 0
Пример №2. x=1-2/3 sqrt(y2-4y-5)
Здесь надо сначала привести к нормальному виду.
3/2(x-1)=sqrt(y2-4y-5)
Возводим в квадрат
9/4(x-1)2=y2-4y-5
9/4x2-9/4*2x+9/4-y2+4y+5=0
9/4x2-9/2x-y2+4y+29/4=0
Далее можно решать как с калькулятором, так и без него:
9/4(x-1)2=y2-4y-5
9/4(x-1)2=y2-4y+4-4-5
9/4(x-1)2=(y2-2)-9
9/4(x-1)2-(y2-2) = -9
-1/4(x-1)2+1/9(y2-2) = 1