Вычисление определителей
Пусть имеется квадратная матрица A размером n x n.Определение. Определителем называется алгебраическая сумма всевозможных произведений элементов, взятых по одному из каждого столбца и каждой строки матрицы A. Если в каждом таком произведении (члене определителя) множители расположены в порядке следования столбцов (т.е. вторые индексы элементов aij в произведении расположены в порядке возрастания), то со знаком (+) берутся те произведения, у которых перестановка первых индексов чётная, а со знаком (-) – те, у которых она нечетная.
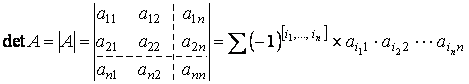
Методы нахождения определителей
- Определитель матрицы разложением по строкам и столбцам через миноры.
- Определитель матрицы методом треугольников
- Определитель матрицы методом понижения порядка
- Определитель методом приведения к треугольному виду (методом Гаусса)
- Определитель матрицы методом декомпозиции
Свойство определителей
- При транспонировании матрицы её определитель не меняется.
- Если поменять местами две строки или два столбца определителя, то определитель изменит знак, а по абсолютной величине не изменится.
- Пусть C = AB где A и B квадратные матрицы. Тогда detC = detA ∙ detB .
- Определитель с двумя одинаковыми строками или с двумя одинаковыми столбцами равен 0. Если все элементы некоторой строки или столбца равны нулю, то и сам определитель равен нулю.
- Определитель с двумя пропорциональными строками или столбцами равен 0.
- Определитель треугольной матрицы равен произведению диагональных элементов. Определитель диагональной матрицы равен произведению элементов стоящих на главной диагонали.
- Если все элементы строки (столбца) умножить на одно и то же число, то определитель умножится на это число.
- Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы) кроме данной, прежние, а в данной строке (столбце) в первом определителе стоят первые, а во втором - вторые слагаемые.
- Теорема Якоби: Если к элементам некоторого столбца определителя прибавить соответствующие элементы другого столбца, умноженные на произвольный множитель λ, то величина определителя не изменится.
- транспонировать матрицу;
- прибавить к какой-либо строке другую строку, умноженную на любое число.
Задание 1. Вычислить определитель, разлагая его по строке или столбцу.
Решение в MS Word. Решение в MS Excel.
Пример 2 в MS Word. Решение в xls.
Задание 2. Вычислить определитель двумя способами: а) по правилу «треугольников»; б) разложением по строке.
Решение.
а) Слагаемые, входящие в со знаком «минус», строятся таким же образом относительно побочной диагонали.
| = |
б) Запишем матрицу в виде:
| A = |
|
∆ = 2 • (0 • 0-2 • 4)-(-1 • (2 • 0-2 • 1))+(-2 • (2 • 4-0 • 1)) = -34
Задание 3. Укажите, чему равен определитель квадратной матрицы A четвертого порядка, если ее ранг r(A)=1.
Ответ: det(A) = 0.




