Интервал сходимости степенного ряда
Назначение сервиса. Онлайн калькулятор предназначен нахождения области сходимости степенного ряда. Результаты вычисления оформляются в формате Word (см. пример).
Например, исходный ряд 
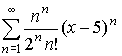подразделяется на три части: n^n, 2^n*n!, (x-5)^n.
Правила ввода функций:
подразделяется на три части: n^n, 2^n*n!, (x-5)^n.
Правила ввода функций:
- Все математические операции выражаются через общепринятые символы (
+,-,*,/,^). Например, (x-4)n, записываем как(x-4)^n. - Число π ≡ pi, корень квадратный √¯ ≡ sqrt. Например, sqrt(n^2+n), en = exp(n)
Здесь будет отображаться решение.
Пример. .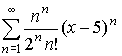
Решение.
Общий вид степенного ряда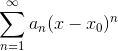 
. В нашем случае x0=5, 
.
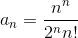Известно, что область сходимости степенного ряда определяется величиной радиуса сходимости R:
|x-x0|<R или x0-R<x<x0+R
Сходимость ряда на границах (при x=x0±R) необходимо исследовать дополнительно.
Найдем радиус сходимости ряда, используя формулу Даламбера:
.
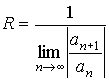Имеем
;
;
.
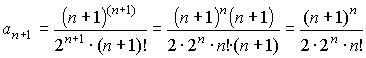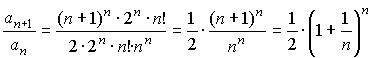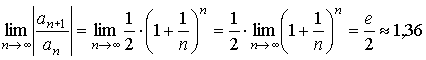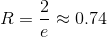
Проверим сходимость ряда при
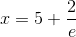. Подставляя это значение в исходный ряд, получим числовой ряд
.
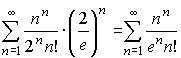Для исследования сходимости этого ряда используем формулу Стирлинга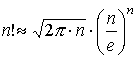 
, верную для факториалов больших чисел.
Получим ряд сравнения. Этот ряд расходится.
Проверим сходимость ряда при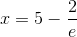 
. Подставляя это значение в исходный ряд, получим числовой ряд
.
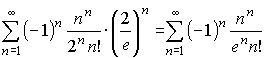Применяя к нему те же соотношения, получим ряд сравнения
.
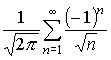Этот ряд сходится (по признаку Лейбница).
Итак, мы получили область сходимости исходного ряда:
.
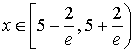