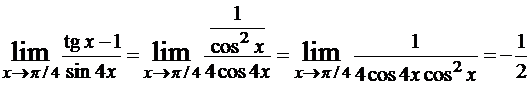Вычисление пределов по правилу Лопиталя
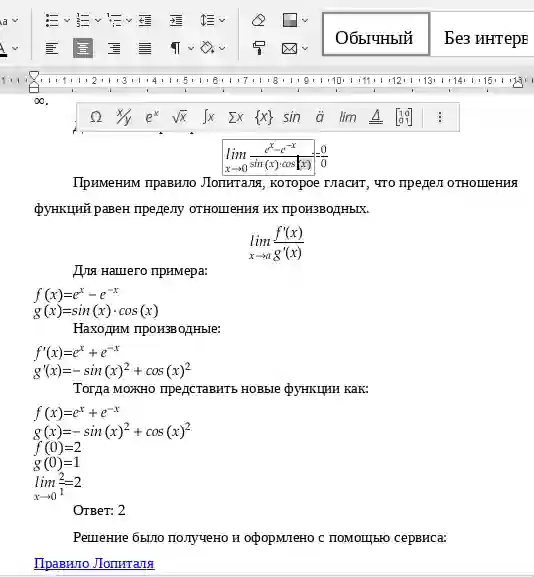
Правило Лопиталя — метод нахождения пределов функций, раскрывающий неопределённости вида 0/0 и ∞/∞. Суть правила: предел отношения функций равен пределу отношения их производных.Назначение сервиса. Данный сервис предназначен для решения пределов, используя правило Лопиталя. Результаты вычисления оформляются в формате Word (см. пример).
Это поле предназначено для ввода числителя дроби.
Правила ввода функций:
x2+3x, записываем как x^2+3*x; ln(1+sin2x) ≡ ln(1+sin(x)^2)
Это поле предназначено для ввода знаменателя дроби. Если знаменатель отсутствует, можно оставить это поле пустым или указать 1.
Правила ввода функций:
Алгоритм вычисления пределов по правилу Лопиталя
Использование правила Лопиталя при нахождении пределов проиллюстрируем следующим примером.Пример. Найти 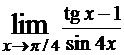 .
.
Решение.Сначала убедимся, что правило Лопиталя применить можно. Действительно, величины, стоящие в числителе и знаменателе при x → π/4 являются бесконечно малыми, то есть имеем неопределенность вида 0/0, следовательно можно воспользоваться правилом Лопиталя: