Асимптоты кривой

Прямая линия называется асимптотой кривой y=f(x), если расстояние точки кривой до этой прямой стремится к нулю при стремлении точки к бесконечности.

Назначение сервиса. Данный сервис предназначен для нахождения асимптот к графику функции в онлайн режиме. Решение оформляется в формате Word.

Правила ввода функции

Примеры

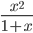≡ x^2/(x+2)
cos²(2x+π) ≡ (cos(2*x+pi))^2

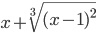≡ x+(x-1)^(2/3)

Скачать пример оформления

Классификация асимптот

Вертикальные асимптоты.
Горизонтальные асимптоты.
Наклонные асимптоты.

Вертикальные асимптоты

Уравнение любой вертикальной прямой, то есть прямой, параллельной оси OY, имеет вид x=a.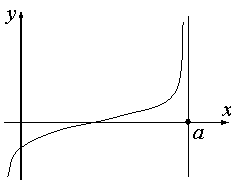

$Вертикальные асимптоты$

Если прямая x=a является вертикальной асимптотой графика функции y=f(x), то очевидно, что хотя бы один из односторонних пределов

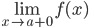или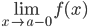

равен бесконечности (+∞ или -∞).
Все функции с бесконечными разрывами (разрывы второго рода) имеют вертикальные асимптоты.

Пример 1. Найти уравнение вертикальных асимптот графика функции .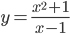
Решение. Видим, что y→∞, если x→1, точнее 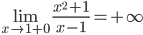, , 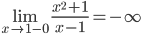то есть прямая x=1 является вертикальной асимптотой, причем двусторонней.

Горизонтальные асимптоты

$Горизонтальные асимптоты$

Всякая горизонтальная прямая имеет уравнение y=A.
Если прямая y=A является горизонтальной асимптотой кривой y=f(x), то

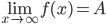Пример 2. Найти горизонтальные асимптоты кривой .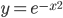
Решение. Найдем 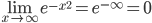, то есть y→0 при x→+∞ и при x→-∞, значит прямая y=0 – горизонтальная асимптота данной кривой.

Наклонные асимптоты

Уравнения наклонных асимптот обычно ищут в виде y=kx+b. По определению асимптоты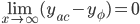

или

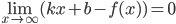(1)
Разделим обе части этого равенства на x:

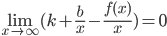, откуда

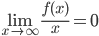(2)
Теперь из (1):

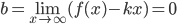(3)
Для существования наклонных асимптот необходимо существование пределов (2) и (3). Если хотя бы один из них не существует, то наклонных асимптот нет. Пределы (2) и (3) нужно находить отдельно при x→+∞ и при x→-∞, так как пределы могут быть разными (функция имеет две разные асимптоты).

Пример 4. Найти наклонные асимптоты графика функции .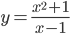
Решение. По формуле (2) найдем .
Теперь найдем 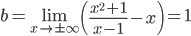. Получаем уравнение наклонной асимптоты y=x+1.

Пример 5. Найти асимптоты кривой y=(x-1)²(x+3).
Решение. Вертикальных и горизонтальных асимптот нет, так как y→∞ при x→∞. Ищем наклонные:
.
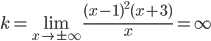Таким образом, кривая асимптот не имеет.

Пример 6. Найти асимптоты кривой .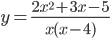
Решение. Поскольку y→∞ при x→0 и при x→4, то прямые x=0 и x=4 являются вертикальными асимптотами. Так как 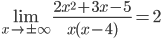, то y=2 – горизонтальная асимптота. Выясним вопрос о существовании наклонных асимптот: 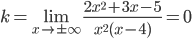, следовательно, кривая наклонных асимптот не имеет (искать “b” не имеет смысла, так как горизонтальные асимптоты уже найдены).

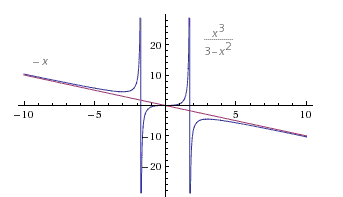
Пример 7. Построить все виды асимптот к функции
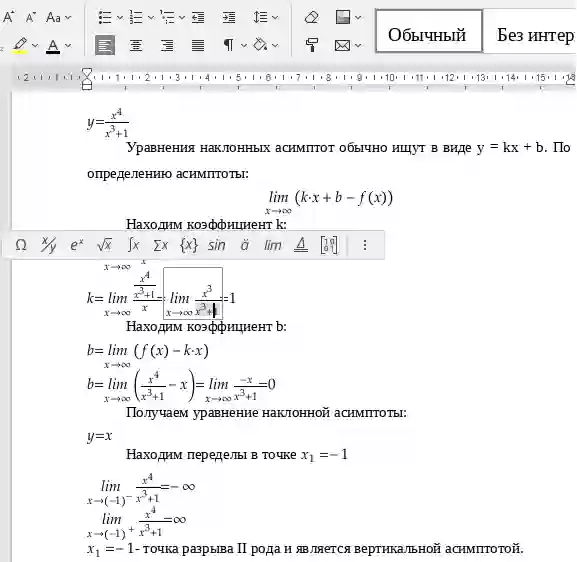
Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:

Находим коэффициент k:

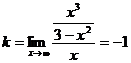
Находим коэффициент b:

Получаем уравнение наклонной асимптоты: y = -x
Найдем вертикальные асимптоты. Для этого определим точки разрыва:

Находим переделы в точке

- является вертикальной асимптотой.
Находим переделы в точке

- является вертикальной асимптотой.