Интервалы выпуклости и вогнутости графика функции
С помощью онлайн-калькулятора можно найти точки перегиба и промежутки выпуклости графика функции с оформлением решения в Word. Является ли функция двух переменных f(x1,x2) выпуклой решается с помощью матрицы Гессе.Направление выпуклости графика функции. Точки перегиба
Определение: Кривая y=f(x) называется выпуклой вниз в промежутке (a; b), если она лежит выше касательной в любой точке этого промежутка.Определение: Кривая y=f(x) называется выпуклой вверх в промежутке (a; b), если она лежит ниже касательной в любой точке этого промежутка.
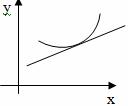
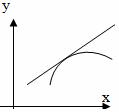
Определение: Промежутки, в которых график функции обращен выпуклостью вверх или вниз, называются промежутками выпуклости графика функции.
Выпуклость вниз или вверх кривой, являющейся графиком функции y=f(x), характеризуется знаком ее второй производной: если в некотором промежутке f’’(x) > 0, то кривая выпукла вниз на этом промежутке; если же f’’(x) < 0, то кривая выпукла вверх на этом промежутке.
Определение: Точка графика функции y=f(x), разделяющая промежутки выпуклости противоположных направлений этого графика, называется точкой перегиба.
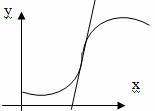
Точками перегиба могут служить только критические точки II рода, т.е. точки, принадлежащие области определения функции y = f(x), в которых вторая производная f’’(x) обращается в нуль или терпит разрыв.
Правило нахождения точек перегиба графика функции y = f(x)
- Найти вторую производную f’’(x).
- Найти критические точки II рода функции y=f(x), т.е. точки, в которой f’’(x) обращается в нуль или терпит разрыв.
- Исследовать знак второй производной f’’(x) в промежутка, на которые найденные критические точки делят область определения функции f(x). Если при этом критическая точка x0 разделяет промежутки выпуклости противоположных направлений, то x0 является абсциссой точки перегиба графика функции.
- Вычислить значения функции в точках перегиба.
Пример 1. Найти промежутки выпуклости и точки перегиба следующей кривой: f(x) = 6x2–x3.
Решение: Находим f ‘(x) = 12x – 3x2, f ‘’(x) = 12 – 6x.
Найдем критические точки по второй производной, решив уравнение 12-6x=0. x=2.

Ответ: Функция выпукла вверх при
x∈(2; +∞); функция выпукла вниз при x∈(-∞; 2); точка перегиба (2;16).
Пример 2. Имеет ли точки перегиба функция: f(x)=x3-6x2+2x-1
Пример 3. Найти промежутки, на которых график функции является выпуклым и выгнутым: f(x)=x3-6x2+12x+4

