Решение дифференциальных уравнений

Уравнение, связывающее независимую переменную, искомую функцию и некоторое количество ее производных, т.е. уравнение вида

F(x,y,y') = 0

называется обыкновенным дифференциальным уравнением n-го порядка.

Например, решить дифференциальное уравнение онлайн: y″-2y+1=sinx. Записываем как y''-2*y+1=sin(x).

Скачать пример отчета

Способы решений дифференциальных уравнений

Уравнения с разделяющимися переменными: y'=e^x+y, xydx+(x+1)dy=0
Однородные уравнения: (y²-2xy)dx+x²dy=0
Постановка задачи о выделении решений.
Калькулятор Линейные уравнения первого порядка: y'+2y=4x
Уравнения Бернулли: y'+2xy=2xy³,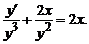
Уравнения в полных дифференциалах: 2xydx+x²dy=0, 2xydx=(x²-y²)dy=0.
Приближенные методы решения дифференциальных уравнений
Уравнения высших порядков
Системы дифференциальных уравнений:
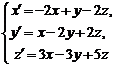
Однородные системы линейных дифференциальных уравнений с постоянными коэффициентами: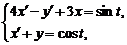
Метод вариации произвольной постоянной

Пример. Найти частное решение дифференциального уравнения y'+xy=x, удовлетворяющего начальному условию y(0)=2.
Решение.
Данное дифференциальное уравнение – уравнение 1-го порядка, линейное относительно неизвестной функции y.
Применяя метод Бернулли для решения этого уравнения, сделаем замену y(x) = u(x)·v(x), где u(x) и v(x) – неизвестные функции, которые мы будем искать поочередно.
Согласно правилу дифференцирования произведения, имеем:
y′ = u′·v+u·v′.
Подставляя выражения для y и y' в исходное уравнение, получим:
u′·v+u·v′ + x·u·v = x (*)
Отсюда
u′·v + (u·v′ + x·u·v) = x;
u′·v + u(v′ + x·v) = x;
Выражение в скобках зависит только от v(x). Будем искать v(x), исходя из условия:
v′ + x·v = 0.
Рассматривая это равенство как дифференциальное уравнение, найдём частное решение для v(x) методом разделения переменных:
; ;
Переходим к интегралу:
; ; .
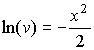Подставим найденную функцию v(x) в уравнение (*):
; .
Найдём теперь общее решение для неизвестной функции u(x):
.
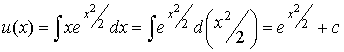Окончательно, имеем общее решение исходного дифференциального уравнения:
.
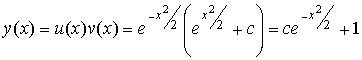Теперь, используем данное начальное условие и найдём частное решение уравнения:
y(0) = c·e⁰+1 = c+1 = 2
Отсюда c=1,
Ответ: частное решение дифференциального уравнения имеет вид: .