Линейные уравнения первого порядка
Уравнение первого порядка видаa1(x)y' + a0(x)y = b(x) называется линейным дифференциальным уравнением. Если b(x) ≡ 0 то уравнение называется однородным, в противном случае - неоднородным. Для линейного дифференциального уравнения теорема существования и единственности имеет более конкретный вид.
Назначение сервиса. Онлайн калькулятор можно использовать для проверки решения однородных и неоднородных линейных дифференциальных уравнений вида y'+y=b(x).
a1(x)y' + a0(x)y = b(x). Например, для y'-exp(x)=2*y это будет y'-2*y=exp(x).
Теорема. Пусть a1(x), a0(x), b(x) непрерывны на отрезке [α,β], a1≠0 для ∀x∈[α,β]. Тогда для любой точки (x0, y0), x0∈[α,β], существует единственное решение уравнения, удовлетворяющее условию y(x0) = y0 и определенное на всем интервале [α,β].
Рассмотрим однородное линейное дифференциальное уравнение a1(x)y'+a0(x)y=0.
Разделяя переменные, получаем 
, или, интегрируя обе части,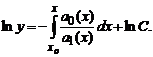 
Последнее соотношение, с учетом обозначения exp(x) = ex, записывается в форме
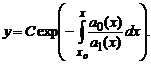
Попытаемся теперь найти решение уравнения в указанном виде, в котором вместо константы C подставлена функция C(x) то есть в виде
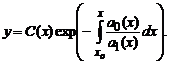
Подставив это решение в исходное, после необходимых преобразований получаем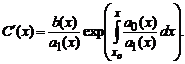 
Интегрируя последнее, имеем
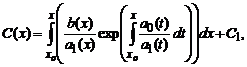
где C1- некоторая новая константа. Подставляя полученное выражение для C(x), окончательно получаем решение исходного линейного уравнения
.
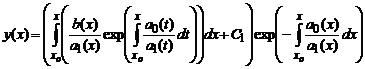Описанный метод решения называется методом Лагранжа или методом вариации произвольной постоянной (см. также Метод вариации произвольной постоянной решения линейных неоднородных уравнений).
Пример. Решить уравнение y' + 2y = 4x. Рассмотрим соответствующее однородное уравнение y' + 2y = 0. Решая его, получаем y = Ce-2x. Ищем теперь решение исходного уравнения в виде y = C(x)e-2x. Подставляя y и y' = C'(x)e-2x - 2C(x)e-2x
в исходное уравнение, имеем C'(x) = 4xe2x, откуда C(x) = 2xe2x - e2x + C1 и y(x) = (2xe2x - e2x + C1)e-2x = 2x - 1 + C1e-2x - общее решение исходного уравнения. В этом решении y1(x) = 2x-1 - движение
объекта под действием силы b(x) = 4x, y2(x) = C1e-2x -собственное движение объекта.
Пример №2. Найти общее решение дифференциального уравнения первого порядка y'+3 y tan(3x)=2 cos(3x)/sin22x.
Это неоднородное уравнение. Сделаем замену переменных: y=u•v, y' = u'v + uv'.
3u v tg(3x)+u v'+u' v = 2cos(3x)/sin22x или u(3v tg(3x)+v') + u' v= 2cos(3x)/sin22x
Решение состоит из двух этапов:
1. u(3v tg(3x)+v') = 0
2. u'v = 2cos(3x)/sin22x
1. Приравниваем u=0, находим решение для 3v tg(3x)+v' = 0
Представим в виде: v' = -3v tg(3x)
Интегирируя, получаем:
ln(v) = ln(cos(3x))
v = cos(3x)
2. Зная v, Находим u из условия: u'v = 2cos(3x)/sin22x
u' cos(3x) = 2cos(3x)/sin22x
u' = 2/sin22x
Интегирируя, получаем: 
Из условия y=u•v, получаем:
y = u•v = (C-cos(2x)/sin(2x)) cos(3x) или y = C cos(3x)-cos(2x) ctg(3x)