Метод вариации произвольной постоянной решения линейных неоднородных уравнений
Рассмотрим теперь линейное неоднородное уравнение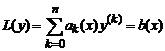 . (2)
. (2)
Пусть y1,y2,.., yn - фундаментальная система решений, а
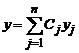 - общее решение соответствующего однородного уравнения
- общее решение соответствующего однородного уравнения L(y)=0. Аналогично случаю уравнений первого порядка, будем искать решение уравнения (2) в виде
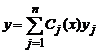 . (3)
. (3)
Убедимся в том, что решение в таком виде существует. Для этого подставим функцию в уравнение. Для подстановки этой функции в уравнение найдём её производные. Первая производная равна
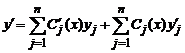 . (4)
. (4)
При вычислении второй производной в правой части (4) появится четыре слагаемых, при вычислении третьей производной - восемь слагаемых и так далее. Поэтому, для удобства дальнейшего счёта, первое слагаемое в (4) полагают равным нулю. С учётом этого, вторая производная равна
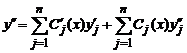 . (5)
. (5)
По тем же, что и раньше, соображениям, в (5) также полагаем первое слагаемое равным нулю. Наконец, n-я производная равна
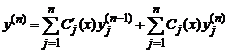 . (6)
. (6)
Подставляя полученные значения производных в исходное уравнение, имеем
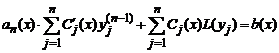 . (7)
. (7)
Второе слагаемое в (7) равно нулю, так как функции yj, j=1,2,..,n, являются решениями соответствующего однородного уравнения L(y)=0. Объединяя с предыдущим, получаем систему алгебраических уравнений для нахождения функций C'j(x)
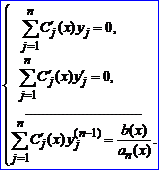 (8)
(8)
Определитель этой системы есть определитель Вронского фундаментальной системы решений y1,y2,..,yn соответствующего однородного уравнения L(y)=0 и поэтому не равен нулю. Следовательно, существует единственное решение системы (8). Найдя его, получим функции C'j(x), j=1,2,…,n, а, следовательно, и Cj(x), j=1,2,…,n Подставляя эти значения в (3), получаем решение линейного неоднородного уравнения.
Изложенный метод называется методом вариации произвольной постоянной или методом Лагранжа.
Пример №1. Найдём общее решение уравнения y'' + 4y' + 3y = 9e-3x. Рассмотрим соответствующее однородное уравнение y'' + 4y' + 3y = 0. Корни его характеристического уравнения r2 + 4r + 3 = 0 равны -1 и -3. Поэтому фундаментальная система решений однородного уравнения состоит из функций y1 = e-x и y2 = e-3x. Решение неоднородного уравнения ищем в виде y = C1(x)e-x + C2(x)e-3x. Для нахождения производных C'1, C'2 составляем систему уравнений (8)
C′1·e-x+C′2·e-3x=0
-C′1·e-x-3C′2·e-3x=9e-3x
решая которую, находим ![]() ,
, ![]() Интегрируя полученные функции, имеем
Интегрируя полученные функции, имеем ![]()
![]()
Окончательно получим ![]()
Скачать пример решения
см. также Решение линейных дифференциальных уравнений онлайн
Пример №2. Решить линейные дифференциальные уравнения второго порядка с постоянными коэффициентами методом вариации произвольных постоянных:
![]()
y(0) =1 + 3ln3
y’(0) = 10ln3
Решение:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r2 -6 r + 8 = 0
D = (-6)2 - 4·1·8 = 4
![]()
Корни характеристического уравнения: r1 = 4, r2 = 2
Следовательно, фундаментальную систему решений составляют функции: y1=e4x, y2=e2x
Общее решение однородного уравнения имеет вид: y=C1·e4x+C2·e2x
Поиск частного решения методом вариации произвольной постоянной.
Для нахождения производных C'i составляем систему уравнений:
C′1·e4x+C′2·e2x=0
C′1(4e4x) + C′2(2e2x) = 4/(2+e-2x)
Выразим C'1 из первого уравнения:
C'1 = -c2e-2x
и подставим во второе. В итоге получаем:
C'1 = 2/(e2x+2e4x)
C'2 = -2e2x/(e2x+2e4x)
Интегрируем полученные функции C'i:
C1 = 2ln(e-2x +2) - e-2x + C*1
C2 = ln(2e2x +1) – 2x+ C*2
Поскольку y=C1·e4x+C2·e2x, то записываем полученные выражения в виде:
C1 = (2ln(e-2x +2) - e-2x + C*1) e4x = 2 e4x ln(e-2x +2) - e2x + C*1 e4x
C2 = (ln(2e2x +1) – 2x+ C*2)e2x = e2x ln(2e2x +1) – 2x e2x + C*2 e2x
Таким образом, общее решение дифференциального уравнения имеет вид:
y = 2 e4x ln(e-2x +2) - e2x + C*1 e4x + e2x ln(2e2x +1) – 2x e2x + C*2 e2x
или
y = 2 e4x ln(e-2x +2) - e2x + e2x ln(2e2x +1) – 2x e2x + C*1 e4x + C*2 e2x
Найдем частное решение при условии:
y(0) =1 + 3ln3
y’(0) = 10ln3
Подставляя x = 0, в найденное уравнение, получим:
y(0) = 2 ln(3) - 1 + ln(3) + C*1 + C*2 = 3 ln(3) - 1 + C*1 + C*2 = 1 + 3ln3
Находим первую производную от полученного общего решения:
y’ = 2e2x(2C1 e2x + C2 -2x +4 e2x ln(e-2x +2)+ ln(2e2x +1)-2)
Подставляя x = 0, получим:
y’(0) = 2(2C1 + C2 +4 ln(3)+ ln(3)-2) = 4C1 + 2C2 +10 ln(3) -4 = 10ln3
Получаем систему из двух уравнений:
3 ln(3) - 1 + C*1 + C*2 = 1 + 3ln3
4C1 + 2C2 +10 ln(3) -4 = 10ln3
или
C*1 + C*2 = 2
4C1 + 2C2 = 4
или
C*1 + C*2 = 2
2C1 + C2 = 2
Откуда: C1 = 0, C*2 = 2
Частное решение запишется как:
y = 2e4x·ln(e-2x +2) - e2x + e2x·ln(2e2x+1) – 2x·e2x + 2·e2x
