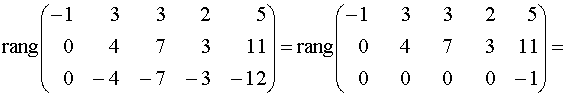Понятие о ранге матрицы
Число r называется рангом матрицы A, если:1) в матрице A есть минор порядка r, отличный от нуля;
2) все миноры порядка (r+1) и выше, если они существуют, равны нулю.
Иначе, ранг матрицы – это наивысший порядок минора, отличного от нуля.
Обозначения: rangA, rA или r.
Из определения следует, что r – целое положительное число. Для нуль-матрицы считают ранг равным нулю.
Назначение сервиса. Онлайн-калькулятор предназначен для нахождения ранга матрицы. При этом решение сохраняется в формате Word и Excel. см. пример решения.
Определение. Пусть дана матрица ранга r. Любой минор матрицы, отличный от нуля и имеющий порядок r, называется базисным, а строки и столбцы его составляющие – базисными строками и столбцами.
Согласно этому определению, матрица A может иметь несколько базисных миноров.
Ранг единичной матрицы E равен n (количеству строк).
Пример 1. Даны две матрицы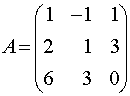 
, 
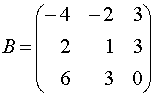и их миноры 
, 
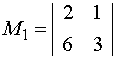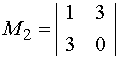. Какой из них можно принять в качестве базисного?
Решение. Минор M1=0, поэтому он не может быть базисным ни для одной из матриц. Минор M2=-9≠0 и имеет порядок 2, значит его можно принять в качестве базисного матриц A или / и B при условии, что они имеют ранги, равные 2. Поскольку detB=0 (как определитель с двумя пропорциональными столбцами), то rangB=2 и M2 можно взять за базисный минор матрицы B. Ранг матрицы A равен 3, в силу того, что detA=-27≠0 и, следовательно, порядок базисного минора этой матрицы должен равняться 3, то есть M2 не является базисным для матрицы A. Отметим, что у матрицы A единственный базисный минор, равный определителю матрицы A.
Теорема (о базисном миноре). Любая строка (столбец) матрицы является линейной комбинацией ее базисных строк (столбцов).
Следствия из теоремы.
- Всякие (r+1) столбцов (строк) матрицы ранга r линейно зависимы.
- Если ранг матрицы меньше числа ее строк (столбцов), то ее строки (столбцы) линейно зависимы. Если rangA равен числу ее строк (столбцов), то строки (столбцы) линейно независимы.
- Определитель матрицы A равен нулю тогда и только тогда, когда ее строки (столбцы) линейно зависимы.
- Если к строке (столбцу) матрицы прибавить другую строку, (столбец) умноженную на любое число, отличное от нуля, то ранг матрицы не изменится.
- Если в матрице зачеркнуть строку (столбец), являющуюся линейной комбинацией других строк (столбцов), то ранг матрицы не изменится.
- Ранг матрицы равен максимальному числу ее линейно независимых строк (столбцов).
- Максимальное число линейно независимых строк совпадает с максимальным числом линейно независимых столбцов.
Пример 2. Найти ранг матрицы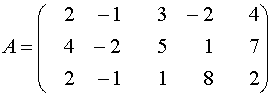 
.
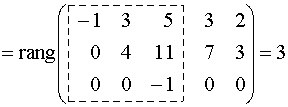
Решение. Исходя из определения ранга матрицы, будем искать минор наивысшего порядка, отличный от нуля. Сначала преобразуем матрицу к более простому виду. Для этого первую строку матрицы умножим на (-2) и прибавим ко второй, затем ее же умножим на (-1) и прибавим к третьей:
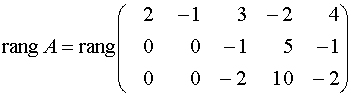
Поскольку вторая и третья строки пропорциональны, то одну из них можно вычеркнуть, что не изменит ранг. Получаем
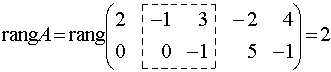, так как в матрице есть минор второго порядка, отличный от нуля, а миноры более высокого порядка отсутствуют.
Пример 3. Привести данную матрицу к ступенчатому виду и определить её ранг.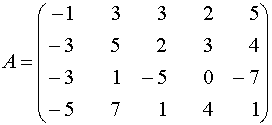 
.
Решение. Получим нули в первом столбце, оперируя первой строкой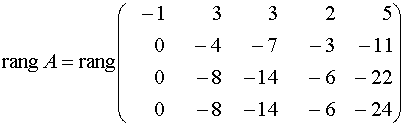 
.
Третью строку вычеркиваем, поскольку она получается умножением второй строки на 2, а в последней строке отбросим общий множитель:
