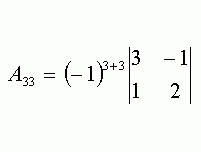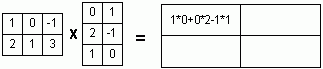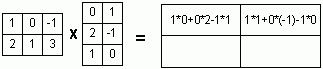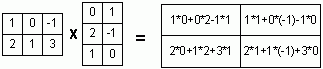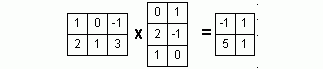Как найти ранг матрицы
Чтобы найти ранг матрицы необходимо привести ее к треугольному виду, с помощью которого можно будет либо найти определитель, либо миноры матрицы. Ранг определителя или минора отличного от нуля и будет являться рангом всей матрицы.
Пример №1. Исходная матрица имеет размерность 3x4.
| 3 | 4 | 2 | 7 |
| 4 | 1 | 2 | 3 |
| 6 | 8 | 4 | 14 |
Решение будем искать с помощью данного калькулятора. Работаем с первым столбцом. Умножим первую строку на 4, а 2-ую строку на (-3). Добавим 2-ую строку к 1-ой.
| 0 | 13 | 2 | 19 |
| 4 | 1 | 2 | 3 |
| 6 | 8 | 4 | 14 |
| 0 | 13 | 2 | 19 |
| 0 | -26 | -4 | -38 |
| 6 | 8 | 4 | 14 |
| 0 | 0 | 0 | 0 |
| 0 | -26 | -4 | -38 |
| 6 | 8 | 4 | 14 |
| 0 | -26 | -4 | -38 |
| 6 | 8 | 4 | 14 |
Пример №2. Рассмотрим пример для матрицы размерностью 3x3.
| 7 | 8 | 1 |
| -2 | 2 | 8 |
| 0 | 1 | 1 |
| 0 | 1 | 1 |
| -2 | 2 | 8 |
| 7 | 8 | 1 |
| 0 | 1 | 1 |
| 0 | 30 | 58 |
| 7 | 8 | 1 |
| 0 | 0 | -28 |
| 0 | 30 | 58 |
| 7 | 8 | 1 |
Количество строк и столбцов матрицы равны, можно найти ее определитель: detA = (-28)·30·7 / 210 = -28 > 0
где z = 7·30 = 210 - произведение чисел, на которые умножали строки матрицы при приведении к треугольному виду (см. как найти определитель методом Гаусса).
Определитель ≠ 0, поэтому ранг матрицы равен количеству строк, т.е. r=3.