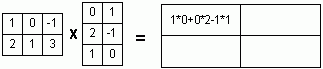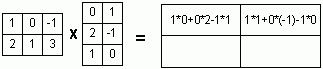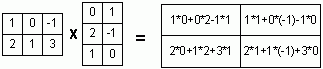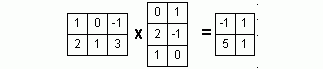Системы линейных уравнений
Назначение сервиса. Онлайн-калькулятор предназначен для исследования системы линейных уравнений. Обычно в условии задачи требуется найти общее и частное решение системы. При исследовании систем линейных уравнений решаются следующие задачи:- является ли система совместной;
- если система совместна, то определенна или неопределенна (критерий совместности системы определяется по теореме);
- если система определенна, то как найти ее единственное решение (используются метод Крамера, метод обратной матрицы или метод Жордана-Гаусса);
- если система неопределенна, то как описать множество ее решений.
Инструкция. Для получения онлайн решения необходимо выбрать
Результат исследования сохраняется в формате Word и Excel (см. пример решения).
Классификация систем линейных уравнений
Произвольная система линейных уравнений имеет вид:a11x1 + a12x2 + ... + a1nxn = b1
a21x1 + a22x2 + ... + a2nxn = b2
...................................................
am1x1 + am2x2 + ... + amnxn = bm
- Системы линейных неоднородных уравнений (количество переменных равно количеству уравнений, m = n).
- Произвольные системы линейных неоднородных уравнений (m > n или m < n).
- Системы линейных однородных уравнений.
Определение. Две системы называются эквивалентными, если решение первой является решением второй и наоборот.
Определение. Система, имеющая хотя бы одно решение, называется совместной. Система, не имеющая ни одного решения, называется несовместной.
Определение. Система, имеющая единственное решение, называется определенной, а имеющая более одного решения – неопределенной.
Алгоритм решения систем линейных уравнений
- Находим ранги основной и расширенной матриц. Если они не равны, то по теореме Кронекера-Капелли система несовместна и на этом исследование заканчивается.
- Пусть rang(A) = rang(B). Выделяем базисный минор. При этом все неизвестные системы линейных уравнений подразделяются на два класса. Неизвестные, коэффициенты при которых вошли в базисный минор, называют зависимыми, а неизвестные, коэффициенты при которых не попали в базисный минор – свободными. Заметим, что выбор зависимых и свободных неизвестных не всегда однозначен.
- Вычеркиваем те уравнения системы, коэффициенты которых не вошли в состав базисного минора, так как они являются следствиями остальных (по теореме о базисном миноре).
- Члены уравнений, содержащие свободные неизвестные, перенесем в правую часть. В результате получим систему из r уравнений с r неизвестными, эквивалентную данной, определитель которой отличен от нуля.
- Полученная система решается одним из способов: метод Крамера, метод обратной матрицы или метод Жордана-Гаусса. Находятся соотношения, выражающие зависимые переменные через свободные.
