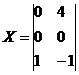Инструкция. Для онлайн решения необходимо выбрать вид уравнения и задать размерность соответствующих матриц.
Матричные уравнения вида (1), (2) и (3) решаются через обратную матрицу A-1. Если задано выражение
A·X - B = C, то необходимо, сначала сложить матрицы C + B, и находить решение для выражения A·X = D, где D = C + B. Если задано выражение A*X = B2, то предварительно матрицу B надо возвести в квадрат.
По координатам вершин треугольника найти площадь, уравнения сторон, уравнение медианы, уравнение биссектрисы
По координатам вершин пирамиды найти
Построение графика функции методом дифференциального исчисления
Экстремум функции двух переменных
Вычисление пределов
Вычисление интегралов
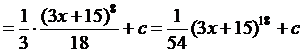
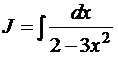
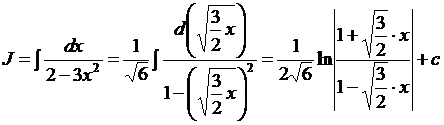
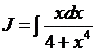
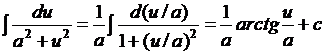
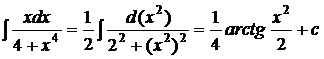
Решение матричных уравнений
Рекомендуется также ознакомиться с основными действиями над матрицами.Пример №1. Задание. Найти решение матричного уравнения ![]()
Решение. Обозначим:
![]()
![]()
![]()
Тогда матричное уравнение запишется в виде: A·X·B = C.
Определитель матрицы А равен detA=-1
Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим слева обе части уравнения на A-1:Умножаем обе части этого равенства слева на A-1 и справа на B-1: A-1·A·X·B·B-1 = A-1·C·B-1. Так как A·A-1 = B·B-1 = E и E·X = X·E = X, то X = A-1·C·B-1
Найдем обратную матрицу A-1.
Транспонированная матрица AT: ![]()
Обратная матрица A-1: ![]()
Найдем обратную матрицу B-1.
Транспонированная матрица BT: ![]()
Обратная матрица
| B-1 = -½ |
|
Матрицу X ищем по формуле: X = A-1·C·B-1
| X = - |
| * |
| -½ |
| = |
|
Ответ:
| X = |
|
Пример №2. Задание. Решить матричное уравнение ![]()
Решение. Обозначим: ![]()
![]()
Тогда матричное уравнение запишется в виде: A·X = B.
Определитель матрицы А равен detA=0
Так как A вырожденная матрица (определитель равен 0), следовательно уравнение решения не имеет.
Пример №3. Задание. Найти решение матричного уравнения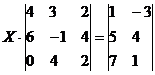
Решение. Обозначим: 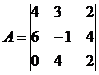
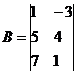
Тогда матричное уравнение запишется в виде: X·A = B.
Определитель матрицы А равен detA=-60
Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим справа обе части уравнения на A-1: X·A·A-1 = B·A-1, откуда находим, что X = B·A-1
Найдем обратную матрицу A-1.
Транспонированная матрица AT: 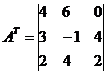
Обратная матрица A-1: 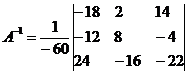
Матрицу X ищем по формуле: X = B·A-1
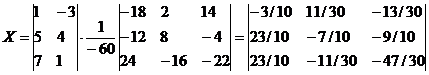
Ответ:
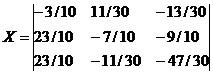
Пример №4. Задание. Решить матричное уравнение 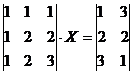
Решение. Обозначим: 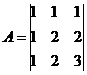
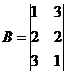
Тогда матричное уравнение запишется в виде: A·X = B.
Определитель матрицы А равен detA=1
Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим слева обе части уравнения на A-1: A-1·A·X = A-1·B, тогда получим E·X = A-1·B, или X = A-1·B.
Найдем обратную матрицу A-1.
Транспонированная матрица AT: 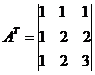
Обратная матрица A-1: 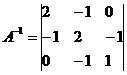
Матрицу Х ищем по формуле: X = A-1·B
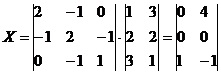
Ответ: