Прямая на плоскости
Построить треугольник, вершины которого находятся в точках A, B, C. По координатам вершин треугольника найти:- координаты точки пересечения медиан;
- длину и уравнение высоты, опущенной из вершины А;
- площадь треугольника;
- систему неравенств, задающих внутренность треугольника АВС.
Инструкция. Для решения подобных задач в онлайн режиме заполните координаты вершин, нажмите Далее. Полученное решение сохраняется в файле Word. см. примеры решений.
Координаты вектора в базисе
Даны вершины A1, A2, A3, A4. По координатам вершин пирамиды найти:
Построение графика функции методом дифференциального исчисления
Экстремум функции двух переменных
Вычисление пределов
Пример №1. В задачах даны координаты точек A,B,C. Требуется: 1) записать векторы AB и AC в системе орт и найти модули этих векторов; 2) найти угол между векторами AB и AC.
Решение.
1) Координаты векторов в системе орт. Координаты векторов находим по формуле:
X=xj-xi; Y=yj-yi
здесь X, Y координаты вектора; xi, yi - координаты точки Аi; xj, yj - координаты точки Аj
Например, для вектора AB: X=x2-x1=12-7=5; Y=y2-y1=-1-(-4)=3
AB(5;3), AC(3;5), BC(-2;2)
2) Длина сторон треугольника. Длина вектора a(X;Y) выражается через его координаты формулой:
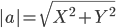
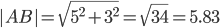
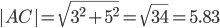
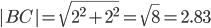
3) Угол между прямыми. Угол между векторами a1(X1;Y1), a2(X2;Y2) можно найти по формуле:
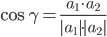
где a1a2=X1X2+Y1Y2
Найдем угол между сторонами AB и AC
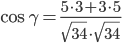
γ = arccos(0.88) = 28.070
8) Уравнение прямой. Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2), представляется уравнениями:
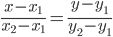
Уравнение прямой AB. Каноническое уравнение прямой:
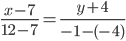или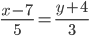 
y=3/5x-41/5 или 5y-3x+41=0
Пример №2.
Вершины треугольника имеют координаты A(1; 3.5), B(16.5; 3.5), C(11; 19). Рассматриваются горизонтальные линии, задаваемые уравнениями y=n, где n - целое.
Найдите сумму длин отрезков, высекаемых на этих прямых сторонами треугольника.
Решение.
- Используя калькулятор, находим уравнения сторон треугольника CA, CB.
Уравнение прямой AC.
Каноническое уравнение прямой: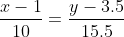
или y = 1.55x + 1.95 или y -1.55x - 1.95 = 0
Уравнение прямой BC
Каноническое уравнение прямой: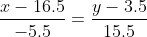
или y = -2.82x + 50 или y + 2.82x - 50 = 0
- Пусть n=15, y=15. Находим точки пересечения с прямыми AC и BC.
Откуда x1 = (15-1.95)/1.55 = 8.42; x2 = (50-15)/2.82 = 12.41{ 15 -1.55x - 1.95 = 0
15 + 2.82x - 50 = 0
Длина отрезка |a|=x2-x1 = 12.41-8.42 = 3.99 ≈ 4
