Деление отрезка в данном отношении
Пусть точки M1, M2, M3 расположены на одной прямой. Говорят, что точка M делит отрезок M1M2 в отношении λ(λ≠-1), если
.
Пусть известны координаты точек M1 и M2 относительно некоторой системы координат: M1(x1, y1, z1), M2(x2, y2, z2), тогда координаты точки M(x, y, z) относительно этой же системы координат находятся по формулам:
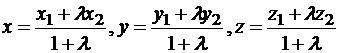. (*)Если точка M находится в середине отрезка M1M2, то
, то есть λ=1 и формулы (*) примут вид:
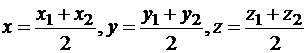(**)Для решения используют следующие калькулятор:
- Точки задаются двумя координатами: A(x1,y1), B(x2,y2).
- Точки задаются тремя координатами: A(x1,y1,z1), B(x2,y2,z2).
Пример №1. Треугольник задан координатами своих вершин A(3, -2, 1), B(3, 1, 5), C(4, 0, 3). Найти координаты D(x, y, z) – точки пересечения его медиан.
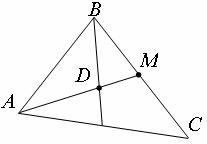
Решение. Обозначим через M(x0, y0, z0) середину BC, тогда по формулам (**)
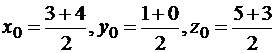и M(7/2, ½, 4). Точка D делит медиану AM в отношении λ=2. Применяя формулы (*), находим
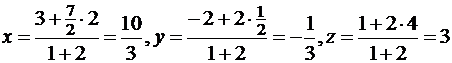
Пример №2. Отрезок AB разделен точкой C(4,1) в отношении λ=1/4, считая от точки A. Найти координаты A, если B(8,5).
Решение. Применяя формулы (*), получим:
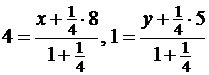, откуда находим x=3, y=0.
Пример №3. Отрезок AB разделен на три равные части точками C(3, -1) и D(1,4). Найти координаты концов отрезка.
Решение. Обозначим A(x1, y1), B(x2, y2). Точка C – середина отрезка AD, следовательно, по формулам (**) находим: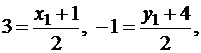 
откуда x1 = 5, y1 = -6. Аналогично находятся координаты точки B: x2 = -1, y2 = 9.