Угол между двумя прямыми
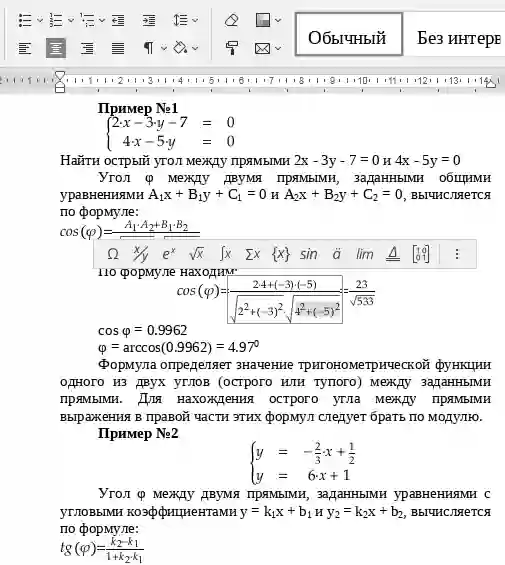
Угол φ между двумя прямыми, заданными общими уравнениями A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0, вычисляется по формуле:Угол φ между двумя прямыми, заданными уравнениями с угловыми коэффициентами y = k1x + b1 и y2 = k2x + b2, вычисляется по формуле:
Угол φ между двумя прямыми, заданными каноническими уравнениями (x-x1)/m1 = (y-y1)/n1 и (x-x2)/m2 = (y-y2)/n2, вычисляется по формуле:
Формулы определяют значение тригонометрической функции одного из двух углов (острого или тупого) между заданными прямыми. Для нахождения острого угла между прямыми выражения в правой части этих формул следует брать по модулю.
Инструкция для нахождения угла между двумя прямыми. Выберите вариант задания исходных данных, нажмите Далее. Полученное решение сохраняется в формате Word.
Пример
Найти угол между двумя прямыми: и
и 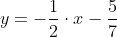
Решение. Угол φ между двумя прямыми, заданными уравнениями с угловыми коэффициентами y = k1x + b1 и y2 = k2x + b2, вычисляется по формуле:

Угловые коэффициенты данных прямых равны -2/3 и -1/2. Воспользуемся формулой, причем ее правую часть берем по модулю:
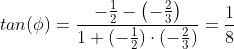
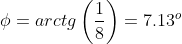
Формула определяет значение тригонометрической функции одного из двух углов (острого или тупого) между заданными прямыми. Для нахождения острого угла между прямыми выражения в правой части этих формул следует брать по модулю.
Точка пересечения прямых:
x=51/7; y=-61/14