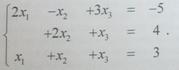Аналитическая геометрия и векторная алгебра
Аналитическая геометрия на плоскости
- Длина отрезка по координатам x,y. Простенький калькулятор, вычисляющий длину вектора по формуле
- По координатам вершин треугольника найти площадь, уравнения сторон, уравнение медианы, уравнение биссектрисы
- Площадь треугольника по координатам вершин.
- Уравнение прямой по координатам вершин.
- Уравнение параллельной прямой. Составляется уравнение прямой, проходящей через точку параллельно данной прямой.
- Уравнение перпендикулярной прямой.
- Угол между двумя прямыми
- Внутренние углы треугольника
- Расстояние от точки до прямой
- Множество точек на плоскости (Составить уравнение множества точек на плоскости)
- Проекция вектора
Аналитическая геометрия в пространстве
- Условие коллинеарности векторов
- Скалярное произведение векторов
- Векторное произведение
- Смешанное произведение векторов
- Момент силы относительно начала координат
По координатам вершин пирамиды. Мощный по своим характеристикам онлайн-калькулятор, который по координатам пирамиды определяет площадь грани, уравнения плоскостей, углы и др.- Площадь параллелограмма, построенного на векторах
- Объем пирамиды, построенной на векторах
- Объем параллелограмма, построенного на векторах
- Угол между двумя плоскостями
- Угол между двумя векторами (прямыми)
Линейная алгебра
- Определитель матрицы
- Матричный калькулятор:
2*A^2-3*A+5*B. - Методы решения системы уравнений: метод Гаусса, метод Крамера, метод обратной матрицы и другие.
- Координаты вектора в новом базисе. Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора в этом базисе.
- Приведение кривой второго порядка к каноническому виду
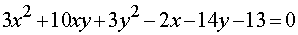
- Собственные числа матрицы
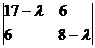
- Выделение полного квадрата (a•x2 + b•x + c = 0)
- Метод неопределенных коэффициентов
- Формула дискриминанта. Данный вид калькулятора используется для нахождения дискриминанта и корней функции.
- Деление многочленов столбиком. Данная процедура, в частности, поможет при нахождении интегралов.
- Решение пределов
Экзаменационный билет №4 по дисциплине «Линейная алгебра и аналитическая геометрия»
1. Линейная зависимость и независимость векторов. Базис на плоскости и в пространстве.Дано: матрица
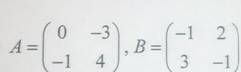Найти их произведение-матрицу C. Для матрицы C найти обратную матрицу.
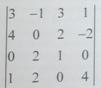
2. Дано: определитель третьего порядка:
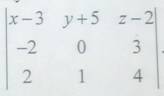Разложить определитель по элементам первой строки.
3. Решить систему линейных алгебраических уравнений методом Гаусса
.
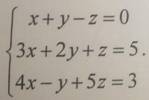4. Дано: векторы
Найти: угол между векторами и векторное произведение заданных векторов.
Примеры решений заданий по векторной алгебре через калькулятор
1. Найдите cos и sin угла между векторами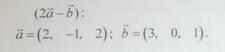
и 
, а также длину вектора 
2. Найдите длину медианы AM в ΔABC, посчитайте площадь этого треугольника. Угол β при вершине B этого треугольника: острый, прямой, тупой?
A(5,-4), B (-3,6), C(1,2).
Методические рекомендации: данную задачу лучше решать через онлайн-калькулятор. Чтобы найти координаты точки пересечения медиан треугольника достаточно найти любые два уравнения медиан, а затем рассчитать точку пересечениях этих прямых.
3. Найдите матрицу A-1, обратную к матрице A, и B(A-1-E):
