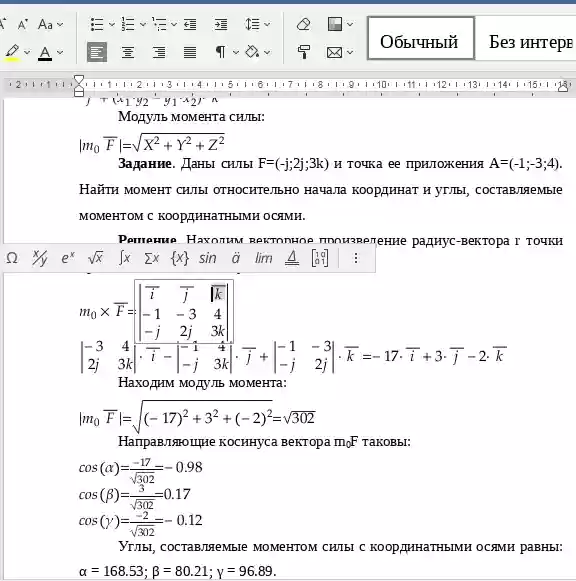
Момент силы относительно начала координат
Если F - сила, а r - радиус-вектор точки е приложения, имеющий начало в точке О, то момент силы F относительно точки О есть вектор, равный векторному произведению r на F, т.е.
Инструкция. Заполните координаты векторов и нажмите кнопку Решение.
Например, для вектора A = 1/3i - 2j + k необходимо ввести: 1/3;-2;1
Пример. Если F - сила, а r - радиус-вектор точки ее приложения, имеющий начало в точке О, то момент силы F относительно точки O есть вектор, равный векторному произведению r на F:
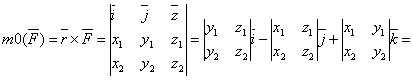
Модуль момента силы:
Задание. Даны силы F=(2;1/2;-1) и точка ее приложения A=(1;-1/2;3). Найти момент силы относительно начала координат и углы, составляемые моментом с координатными осями.
Решение. Находим векторное произведение радиус-вектора r точки приложения силы на силу F:
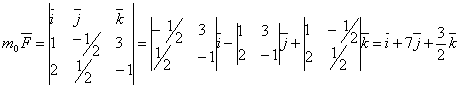
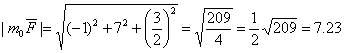
cos α = -1 / 7.23 = -0.14
cos β = 7 / 7.23 = 0.97
cos γ = 3/2 / 7.23 = 0.21
Углы, составляемые моментом силы с координатными осями равны: α = 98.05; β = 14.07; γ = 77.88.
Контрольное вычисление: cos2α + cos2β + cos2γ = (-0.14)2 + 0.972 + 0.212 = 1.
Пример. Модуль силы F равен 60o. Определить момент силы относительно точки O.