Работа силы F при перемещении вдоль дуги линии
Назначение. Онлайн калькулятор предназначен для нахождения работы силы F при перемещении вдоль дуги линии L.
Криволинейные и поверхностные интегралы второго рода
Рассмотрим многообразие σ. Пусть τ(x,y,z)- единичный вектор касательной к σ, если σ - кривая, а n(x,y,z)- единичный вектор нормали к σ, если σ - поверхность в R3. Введём векторы dl=τ·dl и dS=n·dS, где dl и dS - длина и площадь соответствующего участка кривой или поверхности. Будем считать, что dσ=dl, если σ - кривая, и dσ=dS, если σ - поверхность. Назовём dσ ориентированной мерой соответствующего участка кривой или поверхности.Определение. Пусть заданы ориентированное непрерывное кусочно-гладкое многообразие σ и на σ – вектор-функция F(x,y,z)=P(x,y,z)i+Q(x,y,z)+R(x,y,z). Разобьем многообразие на части многообразиями меньшей размерности (кривую – точками, поверхность –кривыми), внутри каждого полученного элементарного многообразия выберем по точке M0(x0,y0,z0), M1(x1,y1,z1), ... ,Mn(xn,yn,zn). Посчитаем значения F(xi,yi,zi), i=1,2,...,n вектор-функции в этих точках,умножим скалярно эти значения на ориентированную меру dσi данного элементарного многообразия (ориентированные длину или площадь соответствующего участка многообразия) и просуммируем. Предел полученных сумм 
если онсуществует, не зависит от способа разбиения многообразия на части и выбора точек внутри каждого элементарного многообразия, при условии, что диаметр элементарного участка стремится к нулю, называется интегралом по многообразию (криволинейным интегралом, если σ -кривая и поверхностным, если σ - поверхность) второго рода, интеграломвдоль ориентированного многообразия, или интегралом от вектора F вдоль σ, и обозначается в общем случае
, в случаях криволинейного и поверхностного интегралов 
соответственно.
Заметим, что если F(x,y,z) - сила, то 
- работа этой силы по перемещению материальной точки вдоль кривой, если F(x,y,z) - стационарное (не зависящее от времени) поле скоростей текущей жидкости, то - количество жидкости, протекающей через поверхность S в единицу времени (поток вектора через поверхность).
Если кривая задана параметрически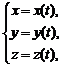 
или, что то же самое, в векторной форме,
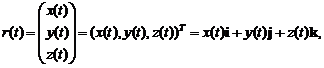
то
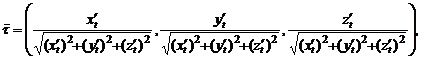
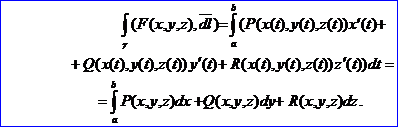
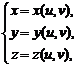или, что тоже самое, в векторной форме
r(u,v)=x(u,v)i+y(u,v)j+z(u,v)k, (u,v)∈D
то
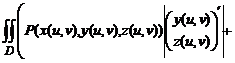
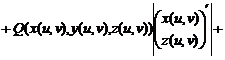
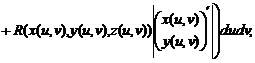
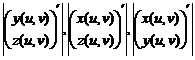- якобианы (определители матриц Якоби, или, что то же самое, матриц производных) вектор-функций 
соответственно.
Если поверхность S может быть задана одновременно уравнениями 
то поверхностный интеграл второго рода вычисляется по формуле
Свойства криволинейного и поверхностного интегралов второго рода
Отметим некоторые свойства криволинейного и поверхностного интегралов второго рода.Теорема 1. Криволинейный и поверхностный интегралы 2-го рода зависят от ориентации кривой и поверхности, точнее
.
Теорема 2. Пусть σ=σ1∪σ2 и размерность пересечения dlim(σ1∩σ2)=n-1. Тогда
Доказательство. Включив в число многообразий разбиения в определении интеграла по многообразию второго рода общую границу σ1 с σ2 получаем требуемое.
Пример №1. Найти работу силы F при перемещении вдоль дуги линии L от точки M0 до точки M1.
F=x2yi+yj;, L: отрезок M0M1
M0(-1;3), M0(0;1)
Решение.
Находим уравнение прямой вдоль отрезка M0M1.
или y=-2x+1
dy=-2dx
Пределы изменения x: [-1; 0]
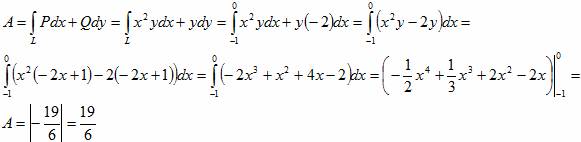
Пример №2. Вычислить 
вдоль кривой 
, если t∈[0;π]
Имеем
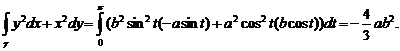
Пример №3. Вычислить поток вектора f(x,y,z)=(yz,xz,xy)T через часть плоскости x+y+z=a лежащую в первом октанте.
Поток вектора через поверхность равен поверхностному интегралу второго рода 
Поверхность однозначно проектируется на все три координатные плоскости. Поэтому интеграл может быть вычислен с помощью проектирования на них. Тогда
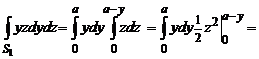
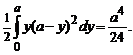Остальные два интеграла считаются аналогично и также равны 
Поэтому поток вектора через поверхность равен 
Знаки плюс перед интегралами взяты потому, что вектор нормали к поверхности составляет острые углы со всеми координатными осями. Поэтому поток вектора через поверхность равен Знаки плюс перед интегралами взяты потому, что вектор нормали к поверхности составляет острые углы со всеми координатными осями.