Как решать задачи по теории вероятностей
В данном разделе приведены онлайн-калькуляторы, с помощью которых решаются основные типовые задачи по теории вероятностей. Решение оформляется в формате Word.Структура дисциплины ТЕОРИЯ ВЕРОЯТНОСТЕЙ
- Задачи про шары. Из урны, где находятся 4 белых и 8 бчерных шаров, случайно вытащены 5 шаров. Какова вероятность того, что среди них будет 2 белых шара?
- Испытания по схеме Бернулли: нахождение биноминального ряда распределения, по которому вычисляются матожидание, дисперсия и среднеквадратическое отклонение
- Формула Пуассона: Какова вероятность при случайном отборе 2000 семян обнаружить 5 семян сорняков?
- Закон распределения случайной величины. На прилавке находится 20 цветов, из которых 12 роз. Для букета отобраны 7 цветов. Найти вероятность того, что букет только из роз.
- Формула полной вероятности: какова вероятность того, что наугад выбранное изделие будет бракованным?
- Наивероятнейшее число событий: рассчитываются вероятности наступления некоторого события: наступит k раз; не менее k1 и не более k2 раз; событие наступит хотя бы один раз.
- Математическое ожидание дискретной случайной величины: нахождение дисперсии и среднеквадратического отклонения. найти математическое ожидание M(X), дисперсию D(X) и среднее квадратическое отклонение σ, если закон распределения случайной величины X задан таблицей:
xi 1 4 5 6 8 pi 0,2 0,1 0,1 0,3 0,3 - Математическое ожидание непрерывной случайной величины: вычисление дисперсии и среднеквадратического отклонения по функции распределения
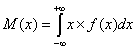
Непрерывная случайная величина Х имеет плотность вероятности f(x). Требуется:
1) найти математическое ожидание;
2) найти дисперсию и среднее квадратическое отклонение;
3) найти функцию распределения вероятностей F(x);
4) построить графики интегральной и дифференциальной функций распределения;
5) найти вероятность попадания значений случайной величины в заданный интервал [a;b].
С помощью калькулятора Web2 можно быстро вычислить некоторые математические выражения.
Примечание:
- 2nd - смена режима
- const - список общепринятых констант (например, постоянная Авогадро, π, масса электрона, постоянная Планка и многие другие).
- ncr - число сочетаний из n по m:
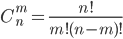
- npr - Число размещений из n элементов по k:
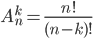
- ! - факториал.
- mod - остаток от деления.
- esc, C - сброс, очистка.
Структура дисциплины МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Основная задача математической статистики – сделать научно обоснованные выводы о распределении одной или более неизвестных случайных величин или их взаимосвязи между собой.- Корреляционная таблица. Распределение 175 элементов по признаку X и признаку Y дано в таблице. Найти: а) уравнение регрессии Y по X и X по Y; б) коэффициент корреляции между Y и X.
- Системы случайных величин: X и Y. Найти линейную среднюю квадратическую регрессию случайной величины Y на случайную величину X на основе заданного закона распределения двумерной случайной величины.
- Выборочный метод: оценка среднего значения, дисперсия, доверительные интервалы.
Типы решаемых задач:
- Задание 1. Для изучения количественного дискретного признака Х из генеральной совокупности извлечена выборка. Требуется:
- составить вариационный ряд;
- найти статистическое распределение выборки в виде распределения частот, построить полигон частот;
- найти распределение относительных частот и построить полигон относительных частот;
- найти эмпирическую функцию распределения по данным вариационного ряда, построить график;
- найти выборочную среднюю; найти выборочную дисперсию; найти «исправленную» выборочную дисперсию.
- Задание 2. Найти методом сумм выборочную среднюю и выборочную дисперсию по заданному распределению выборки объема N.
- Задание 1. Для изучения количественного дискретного признака Х из генеральной совокупности извлечена выборка. Требуется:
- Доверительный интервал: для генерального среднего значения, для математического ожидания, для генеральной доли.
Оценивается концентрация примеси некоторого вещества в исследуемом материале. Получены следующие результаты. Найти доверительные интервалы для средней концентрации данного вещества с надежностью 0,95 и среднеквадратического отклонения от среднего значения с надежностью 0,99. Принять, что результаты измерений распределены по нормальному закону. - Уравнение регрессии: y = ax + b
Пример №1. Данные опыта приведены в таблице в безразмерном виде. Полагая, что x и y связаны зависимостью y = ax + b определить коэффициенты a и b методом наименьших квадратов.
Пример №2. Экономист, изучая зависимость уровня издержек обращения Y (тыс. руб.) от объема товарооборота Х (тыс. руб.), обследовал 10 магазинов, торгующих одинаковым ассортиментом товаров, и получил следующие данные. Полагая, что между признаками X и Y имеет место линейная корреляционная связь, определить выборочное уравнение линейной регрессии y(x) = b0 + b1(x - xср) и выборочный коэффициент линейной корреляции rxy. Построить диаграмму рассеяния и линию регрессии. Сделать вывод о направлении и тесноте связи между признаками X и Y. Используя полученное уравнение линейной регрессии, оценить ожидаемое среднее значение признака Y при х*=130 тыс. руб. - Проверка гипотезы о виде распределения: нормальное распределение, распределение Пуассона, биномиальное распределение, показательное распределение, равномерное распределение.
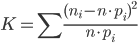 . Пример. Произведено N=200 испытаний, в результате каждого из которых событие А появлялось в различные моменты времени. В итоге было получено эмпирическое распределение, приведенное в табл.37 (в первом столбце указаны интервалы времени в минутах, во втором столбце — соответствующие частоты, т.е.число появлений события А в интервале). Требуется при уровне значимости 0,05 проверить гипотезу о том, что время появления событий распределено равномерно.
. Пример. Произведено N=200 испытаний, в результате каждого из которых событие А появлялось в различные моменты времени. В итоге было получено эмпирическое распределение, приведенное в табл.37 (в первом столбце указаны интервалы времени в минутах, во втором столбце — соответствующие частоты, т.е.число появлений события А в интервале). Требуется при уровне значимости 0,05 проверить гипотезу о том, что время появления событий распределено равномерно.
- Проверка гипотезы о равенстве дисперсий и генеральных средних.
- Проверка статистических гипотез: гипотеза о генеральном среднем значении нормального распределения при не известной дисперсии.
- Однофакторный дисперсионный анализ: методом дисперсионного анализа при уровне значимости 0.05 проверить нулевую гипотезу о равенстве групповых средних. Пример. Для изучения величины X произведено 4 испытания на каждом из пяти уровней фактора F. Результаты испытаний приведены в таблице. Выяснить, существенно ли влияние фактора F на величину X. Принять α = 0.05. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
- Двухфакторный дисперсионный анализ.
