Доверительный интервал
Доверительный интервал – предельные значения статистической величины, которая с заданной доверительной вероятностью γ будет находится в этом интервале при выборке большего объема. Обозначается как P(θ - ε < x < θ + ε) = γ. Мерой доверия оценке θ считается вероятность γ того, что погрешность оценки |θ - x| не превысит заданной точности ε:
. На практике выбирают доверительную вероятность γ из достаточно близких к единице значений γ = 0.9, γ = 0.95, γ = 0.99.
Назначение сервиса. С помощью этого сервиса определяются:
- доверительный интервал для генерального среднего, доверительный интервал для дисперсии;
- доверительный интервал для среднего квадратического отклонения, доверительный интервал для генеральной доли;
В некоторых расчетах потребуется найти необходимый объем выборки при известной доле и точности.
Пример №2. Из партии импортируемой продукции на посту Московской Северной таможни было взято в порядке случайной повторной выборки 20 проб продукта «А». В результате проверки установлена средняя влажность продукта «А» в выборке, которая оказалась равной 6 % при среднем квадратическом отклонении 1 %.
Определите с вероятностью 0,683 пределы средней влажности продукта во всей партии импортируемой продукции.
Пример №3. Опрос 36 студентов показал, что среднее количество учебников, прочитанных ими за учебный год, оказалось равным 6. Считая, что количество учебников, прочитанных студентом за семестр, имеет нормальный закон распределения со средним квадратическим отклонением, равным 6, найти: А) с надежностью 0,99 интервальную оценку для математического ожидания этой случайной величины; Б) с какой вероятностью можно утверждать, что среднее количество учебников, прочитанных студентом за семестр, вычисленное по данной выборке, отклонится от математического ожидания по абсолютной величине не больше, чем на 2.
Классификация доверительных интервалов
По виду оцениваемого параметра:
- Доверительный интервал для генерального среднего (математического ожидания);
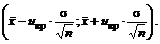
- Доверительный интервал для дисперсии:
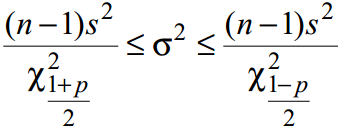
где s2 - выборочная дисперсия; Χ2 - квантиль распределения Пирсона. - Доверительный интервал для среднеквадратического отклонения;
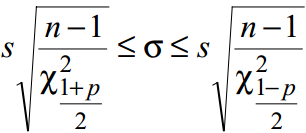
- Доверительный интервал для генеральной доли;
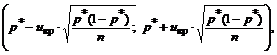
По типу выборки:
- Доверительный интервал для бесконечной выборки;
- Доверительный интервал для конечной выборки;
| Генеральная совокупность | Бесконечная | Конечная объема N |
| Тип отбора | Повторный | Бесповторный |
| Средняя ошибка выборки |  |
 |
По виду критической области:
1-α - доверительный интервал- двусторонняя: (-∞, Χα/2) ∪ (Χα/2, +∞ )
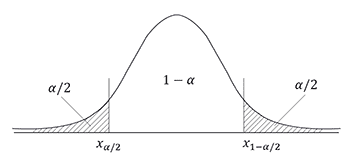
- левосторонняя: (-∞, Χα)
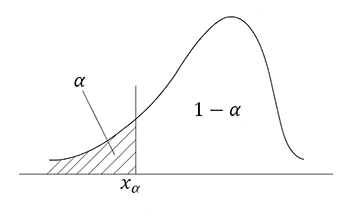
- правосторонняя: (Χ1-α, +∞)
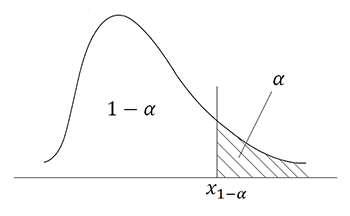
Площадь заштрихованной области равна p-уровню (p - это вероятность отвергнуть нулевую гипотезу при условии, что она верна).
В MS Excel это значение вычисляется:
- двусторонняя область:
=2*(1-НОРМСТРАСП(Χнабл)) - левосторонняя область:
=НОРМСТРАСП(Χнабл) - правосторонняя область:
=1-НОРМСТРАСП(Χнабл)
Примеры применения
Расчет средней ошибки выборки при случайном отборе
Расхождение между значениями показателей, полученных по выборке, и соответствующими параметрами генеральной совокупности называется ошибкой репрезентативности.Обозначения основных параметров генеральной и выборочной совокупности.
| Характеристики | Генеральная совокупность | Выборочная совокупность |
| Объем совокупности (численность единиц) | N | n |
| Численность единиц, обладающих обследуемым качеством (признаком) | M | m |
| Доля единиц, обладающих обследуемым качеством (признаком), выборочная доля | 
| 
|
| Формулы средней ошибки выборки | |||
| повторный отбор | бесповторный отбор | ||
| для средней | для доли | для средней | для доли |
| 
| 
| 
|
или Δ = t·μ, где t– коэффициент доверия, определяемый в зависимости от уровня вероятности Р(t) по таблице интегральной функции Лапласа.
Формулы расчета численности выборки при собственно-случайном способе отбора
| Способ отбора | Формулы определения численности выборки | ||
| для средней | для доли | ||
| Повторный |  |  | |
| Бесповторный |  | 
| |
Метод доверительных интервалов
Алгоритм нахождения доверительного интервала включает следующие шаги:- задается доверительная вероятность γ (надежность).
- по выборке определяется оценка параметра a.
- из соотношения
P(α1 < a < α2) = γнаходится ошибка ε. - рассчитывается доверительный интервал (a - ε ; a + ε).
Пример №1. При проверке годности партии таблеток (250 шт.) оказалось, что средний вес таблетки 0,3 г, а СКО веса 0,01 г. Найти доверительный интервал, в который с вероятностью 90% попадает норма веса таблетки.
Решение.
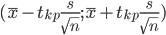
Определяем значение tkp по таблицам функции Лапласа.
В этом случае 2Ф(tkp) = 1 - γ
Ф(tkp) = γ/2 = (1- 0.05)/2 = 0.475
По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 0.475
tkp(γ) = Ф(0.475) = 1.96
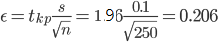
(0.3 - 0.206;0.3 + 0.206) = (0.094;0.51)
С вероятностью 0.9 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала.
Пример №2. На площади в 70 га, занятой пшеницей, определяется с помощью выборочного метода доля посева, пораженная насекомыми вредителями. Сколько проб надо взять в выборку, чтобы при вероятности 0,997 определить искомую величину с точностью до 4%, если пробная выборка показывает, что доля пораженной посевной площади составляет 9%?
Решение ищем по формуле определения численности выборки для повторного отбора.
Ф(tkp) = γ/2 = 0.997/2 = 0,4985 и этому значению по таблице Лапласа соответствует tkp =2.96.
w = 9% = 0,09
Δ = 4% = 0,04
Итого: n = 2.962*0,09(1-0,09)/0,042 = 448,4844 ≈ 449
Пример. При проверке веса импортируемого груза на таможне методом случайной повторной выборки было отобрано 100 изделий. В результате был установлен средний вес изделия 5000 г при среднем квадратическом отклонении 40 г. С вероятностью 0,950 определить пределы, в которых находится средний вес изделия в генеральной совокупности.
Решение
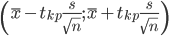
Поскольку n>30, то определяем значение tkp по таблицам функции Лапласа.
В этом случае 2Ф(tkp) = γ
Ф(tkp) = γ/2 = 0.95/2 = 0.475
По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 0.475
tkp(γ) = (0.475) = 1.96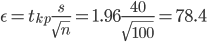
(5000 - 78.4;5000 + 78.4) = (4921.6;5078.4)
С вероятностью 0.95 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала.
Пример. С надежностью γ=0.954 построить доверительный интервал для генеральной доли
Пример №1
Пример. По результатам выборочного наблюдения (выборка В приложение) вычислите несмещенные оценки среднего значения, дисперсии и среднего квадратического отклонения генеральной совокупности.
Скачать решение
Пример. Найдите доверительные интервалы для оценки среднего значения и среднего квадратического отклонения генеральных совокупностей при доверительной вероятности y, если из генеральных совокупностей сделана выборка В и y.
Скачать решение
Пример.
1. Используя результаты расчетов, выполненных в задании № 2 и полагая, что эти данные получены при помощи собственно-случайного 10-ти процентного бесповторного отбора, определить:
а) пределы, за которые с доверительной вероятностью 0,954 не выйдет среднее значение признака, рассчитанное по генеральной совокупности;
б) как нужно изменить объем выборки, чтобы снизить предельную ошибку средней величины на 50%.
2. Используя результаты расчетов, выполненных в задании № 2 и полагая, что эти данные получены при помощи повторного отбора, определить:
а) пределы, за которые в генеральной совокупности не выйдет значение доли предприятий, у которых индивидуальные значения признака превышают моду с доверительной вероятностью 0,954;
б) как изменить объем выборки, чтобы снизить предельную ошибку доли на 20 %.
Методические указания
Задание. Поточная линия по производству однотипных деталей подвергалась реконструкции Заданы две выборки отображающие процент брака в партиях деталей выпускаемых на данной линии до и после реконструкции Можно ли достоверно утверждать, что после реконструкции процент брака в партиях деталей снизился?
Пример. Ниже приведены данные по затратам на бурение (у.е.) для 49 скважин Западно-Сибирской нефтяной базы России:
| 129 | 142 | 132 | 61 | 96 | 96 | 142 | 17 | 135 | 32 |
| 77 | 58 | 37 | 132 | 79 | 15 | 145 | 64 | 83 | 120 |
| 11 | 54 | 48 | 100 | 43 | 25 | 67 | 25 | 140 | 130 |
| 48 | 124 | 29 | 107 | 135 | 101 | 93 | 147 | 112 | 121 |
| 89 | 97 | 60 | 84 | 46 | 139 | 43 | 145 | 29 |
- провести выборку собственно случайным способом объемом n=5;
- определить интервальные значения среднего генеральной совокупности (X) по рассчитанным выборочным показателям (X, s2) с помощью функции t-распределения Стьюдента при уровне значимости α=0.05;
- определить точечное значение среднего генеральной совокупности (X) по исходным данным;
- оценить правильность интервальных расчетов, сравнивая точечное значение (X) с интервальным значением, рассчитанным по выборке;
1. Выбираем 5 значений из таблицы. Пусть это будет 3 столбец: 132, 37, 48, 29, 60.
В разделе «Вид статистического ряда» выбираем Дискретный ряд. В поле Количество строк указываем 5.
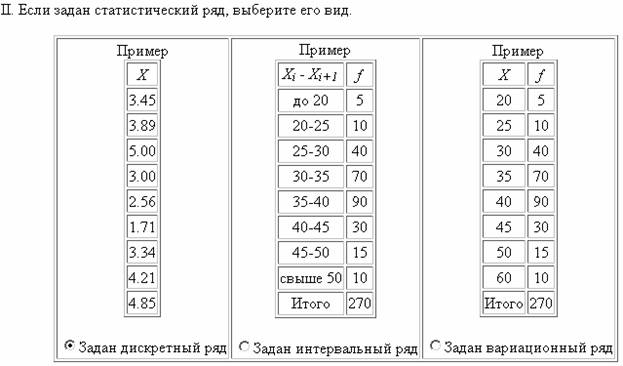
2. Вводим исходные данные.
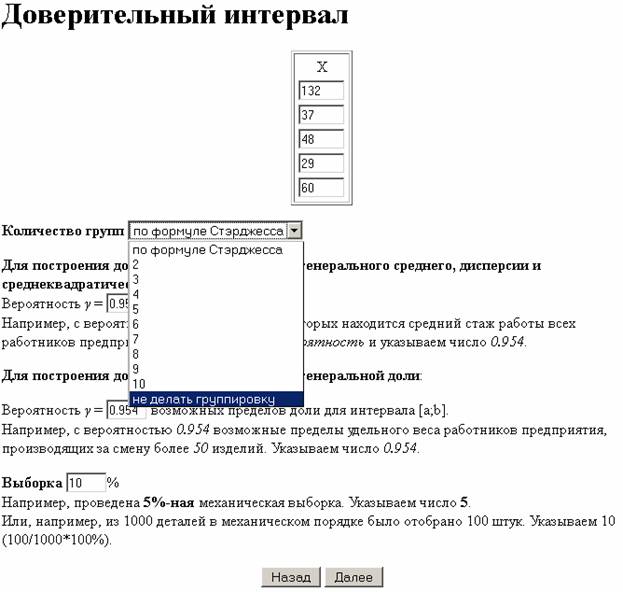
Поле «Доверительный интервал генерального среднего, дисперсия и среднеквадратическое отклонения» указываем значение γ = 0.95 (что соответствует α=0.05).
В поле «Выборка» указываем значение 10 (поскольку из 49 значений выбрали 5, что соответствует 10,2% (5/49x100%)).
В разделе «Выводит в отчет» отмечаем первый пункт «Доверительный интервал для генерального среднего».
Нажимаем кнопку Далее.
3. Полученное решение сохраняется в формате Word (скачать).
Задание №2: В целях изучения затрат времени на изготовление одной детали рабочими завода проведена 10%-ная случайная бесповторная выборка, в результате которой получено распределение деталей по затратам времени, представленное в прил. Б.
Решение.
Задание №3: Используя результаты расчетов, выполненных в задании №2 и полагая, что эти данные получены при помощи повторного отбора, определить:
Решение.
Задание №4: Из партии электроламп взята 20%-ная случайная бесповторная выборка для определения среднего веса спирали. Результаты выборки следующие.
Вес, мг:38-40;40-42;42-44;44-46.
Число спиралей:15;30;45;10.
Определить с вероятностью 0.95 доверительные пределы, в которых лежит средний вес спирали, для всей партии электроламп.
Решение.
Задание №5: На заводе электроламп из партии продукции в количестве 16000 шт. ламп взято на выборку 1600 шт. (случайный, бесповторный отбор), из которых 40 шт. оказались бракованными.
Определить с вероятностью 0.997 пределы, в которых будет находиться процент брака для всей партии продукции.
Решение.
Перед расчетами создается предварительная таблица, в которой подсчитывается количество повторений значений Х.
В данном случае все значения X встречаются ровно один раз. Интервальные значения среднего генеральной совокупности рассчитываются в разделе «Интервальное оценивание центра генеральной совокупности».
x (x - x ср)2 29 1036.84 37 585.64 48 174.24 60 1.44 132 5012.64
306 6810.8
Примечание: в данном случае в расчетах используется Оценка среднеквадратического отклонения.
На основании этих данных вычислите:
а) средние затраты времени на изготовление одной детали;
б) средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение;
в) коэффициент вариации;
г) с вероятностью 0,954 предельную ошибку выборочной средней и возможные границы, в которых ожидаются средние затраты времени на изготовление одной детали на заводе;
д) с вероятностью 0,954 предельную ошибку выборочной доли и границы удельного веса числа деталей с минимальными затратами времени на их изготовление. Перед тем как производить расчеты, необходимо записать условия задачи и заполнить табл. 2.1
Для получения решения указываем следующие параметры:
а) пределы, за которые в генеральной совокупности не выйдет значение доли предприятий, у которых индивидуальные значения признака превышают моду с доверительной вероятностью 0.954;
б) как изменить объем выборки, чтобы снизить предельную ошибку доли на 20%.
Используя результаты расчетов, выполненных в задании № 2 и полагая, что эти данные получены при помощи повторного отбора, определить:
а) пределы, за которые в генеральной совокупности не выйдет значение доли предприятий, у которых индивидуальные значения признака превышают моду с доверительной вероятностью 0.954;
б) как изменить объем выборки, чтобы снизить предельную ошибку доли на 20%.
Вводим следующие параметры:
Здесь N = 16000, n = 1600, w = d / n = 40/1600 = 0.025.
