F-статистика. Критерий Фишера
Начало решения см. здесь. На данном примере рассмотрим, как оценивается надежность полученного уравнение регрессии. Этот же тест используется для проверки гипотезы о том, что коэффициенты регрессии одновременно равны нулю, a=0, b=0. Другими словами, суть расчетов - ответить на вопрос: можно ли его использовать для дальнейшего анализа и прогнозов?Для установления сходства или различия дисперсий в двух выборках используйте данный t-критерий.
Перейти к онлайн решению своей задачи
Итак, целью анализа является получение некоторой оценки, с помощью которой можно было бы утверждать, что при некотором уровне α полученное уравнение регрессии - статистически надежно. Для этого используется коэффициент детерминации R2.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
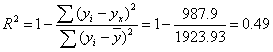
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R2=0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
![]()
![]()
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2 (или через функцию Excel FРАСПОБР(вероятность;1;n-2)).
Fтабл - это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости α. Уровень значимости α - вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно α принимается равной 0,05 или 0,01.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=48, Fтабл = 4
Выводы: Поскольку фактическое значение F > Fтабл, то коэффициент детерминации статистически значим (найденная оценка уравнения регрессии статистически надежна).
Дисперсионный анализ
.| Источник вариации | Сумма квадратов | Число степеней свободы | Дисперсия на 1 степень свободы | F-критерий |
| Модель | 936.03 | 1 | 936.03 | 45.48 |
| Остаточная | 987.9 | 48 | 20.58 | 1 |
| Общая | 1923.93 | 50-1 |
Показатели качества уравнения регрессии
| Показатель | Значение |
| Коэффициент детерминации | 0.49 |
| Средний коэффициент эластичности | 0.51 |
| Средняя ошибка аппроксимации | 10.89 |
Пример. По совокупности 25 предприятий торговли изучается зависимость между признаками: X — цена на товар А, тыс. руб.; Y — прибыль торгового предприятия, млн. руб. При оценке регрессионной модели были получены следующие промежуточные результаты: ∑(yi-yx)2 = 46000; ∑(yi-yср)2 = 138000. Какой показатель корреляции можно определить по этим данным? Рассчитайте величину этого показателя, на основе этого результата и с помощью F-критерия Фишера сделайте вывод о качестве модели регрессии.
Решение. По этим данным можно определить эмпирическое корреляционное отношение: 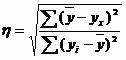 , где ∑(yср-yx)2 = ∑(yi-yср)2 - ∑(yi-yx)2 = 138000 - 46000 = 92 000.
, где ∑(yср-yx)2 = ∑(yi-yср)2 - ∑(yi-yx)2 = 138000 - 46000 = 92 000.
η2 = 92 000/138000 = 0.67, η = 0.816 (0.7 < η < 0.9 - связь между X и Y высокая).
F-критерий Фишера: n = 25, m = 1.
R2 = 1 - 46000/138000 = 0.67, F = 0.67/(1-0.67)x(25 - 1 - 1) = 46. Fтабл(1; 23) = 4.27
Поскольку фактическое значение F > Fтабл, то найденная оценка уравнения регрессии статистически надежна.
Вопрос: Какую статистику используют для проверки значимости модели регрессии?
Ответ: Для значимости всей модели в целом используют F-статистику (критерий Фишера).

