Примеры решений задач по эконометрике
В этом разделе собраны типовые примеры решения задач по статистике. Как правило, после каждого решения следует ссылка на онлайн-калькулятор, с помощью которого можно решить данную задачу.Парная регрессия и корреляция
- Оценка параметров уравнения регрессии
- Пример нахождения коэффициента корреляции (линейный коэффициент корреляции Пирсона). Значимость коэффициента корреляции.
- Пример нахождения доверительных интервалов коэффициентов регрессии
- Пример нахождения коэффициента детерминации
- Пример нахождения статистической значимости коэффициентов регрессии (параметров регрессии)
- Средняя ошибка аппроксимации
По семи территориям Уральского района За 199Х г. известны значения двух признаков.
По территориям региона приводятся данные за 199Х г. - Парная нелинейная регрессия и корреляция
Изучается зависимость материалоемкости продукции от размера предприятия по 10 однородным заводам (см. таблицу). - Экспоненциальное уравнение регрессии
Парная нелинейная регрессия и корреляция
- Парная нелинейная регрессия и корреляция
Изучается зависимость материалоемкости продукции от размера предприятия по 10 однородным заводам (см. таблицу). - Экспоненциальное уравнение регрессии
- Индекс корреляции (для нелинейной связи)
- Другие примеры для нелинейной связи (Аналитическое выравнивание ряда по параболе, степенной функции)
Регрессионный и корреляционный анализа
- Пример регрессионного анализа
- Корреляционный анализ
- Поле корреляции и формулирование гипотезы о форме связи
По территории Северного, Северо-Западного и Центрального районов известны данные за ноябрь 1997 г. - Решение контрольной работы по эконометрике
По 12 предприятиям концерна изучается зависимость прибыли (тыс. руб.) Y от выработки продукции на одного человека (единицу) по следующим данным (см. таблицу) - Практикум по эконометрике
- Методические рекомендации по подготовке контрольных работ
Исследовать статистическую зависимость между парой показателей:Х{ 10, 22, 15, 22, 7, 14, 20} и Y{5, 1, 3, 2, 7, 4, 1 } - Эконометрическое исследование
- Тест Голдфелда-Квандта
- Пример проверки наличия в модели автокорреляции
- Частные F-критерии
Непараметрические показатели связи
- Пример нахождения коэффициента ранговой корреляции Спирмена
- Коэффициент ранговой корреляции Кендалла
- Проверка на гетероскедастичность при помощи теста ранговой корреляции Спирмена
- Коэффициент корреляции знаков
Эконометрические методы проведения экспертных исследований
- Метод средних баллов.
- Медианный метод.
- Расчет коэффициента конкордации.
- Пример расчета коэффициента контингенции.
Статистические таблицы
- Шкала Чеддока. Применяется для оценки показателей тесноты связи (коэффициента линейной корреляции, коэффициента Фехнера, коэффициента ранговой корреляции Спирмена).
- Статистические таблицы Стьюдента и Фишера. используются для оценки качества полученного уравнения регрессии.
- Статистические таблицы Дарбина-Уотсона. используется для анализа автокорреляции.
- Распределение ХИ квадрат (X
2 ). Используется для определения доверительного интервала дисперсии и проверке гипотез о виде распределения. - Критические значения критерия U Манна-Уитни.
Эконометрический анализ в Excel
Оформление решений
Оформление отчета по форме №2
tкрит(n-m-1;α/2) = tкрит(8;0.025) = 2.752tb=bmb
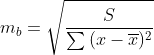
ta=ama
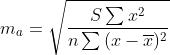
Доверительный интервал для коэффициентов уравнения регрессии.
Для расчета доверительного интервала определяем предельную ошибку Δ для каждого показателя:
Δb = ±tтаблmb = ±2.752*0.441 = 1.213
Доверительный интервал: b - Δb ≤ b ≤ b + Δb
5.22 - 1.213 ≤ b ≤ 5.22 + 1.213
1.089 ≤ b ≤ 3.515
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
Δa = ±tтаблma = ±2.752*36.855 = 101.426
Доверительный интервал: a - Δa ≤ a ≤ a + Δa
3.56 - 101.426 ≤ a ≤ 3.56 + 101.426
-232.492 ≤ a ≤ -29.64
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
Список литературы
- Орлова И.В., Половников В.А. Экономико-математические методы и модели: компьютерное моделирование: учебное пособие. – М.: Вузовский учебник, 2007, 2011.(любое издание, но лучше третье)
- Костюнин В.И. Эконометрика. Учебник и практикум для прикладного бакалавриата – М.: Юрайт, 2015
- Кремер Н.Ш., Путко Б.А. Эконометрика: учебник для вузов / под ред. проф. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2003–2008
- Эконометрика: учебник / под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005–2008.
