Пример нахождения коэффициента ранговой корреляции Спирмена
На практике для определения тесноты связи двух признаков часто применяется коэффициент ранговой корреляции Спирмена (Р). Значения каждого признака ранжируются по степени возрастания (от 1 до n), затем определяется разница (d) между рангами, соответствующими одному наблюдению.Пример №1. Зависимость между объемом промышленной продукции и инвестициями в основной капитал по 10 областям одного из федеральных округов РФ в 2003 году характеризуется следующими данными.
Вычислите ранговые коэффициенты корреляции Спирмена и Кендэла. Проверить их значимость при α=0,05. Сформулируйте вывод о зависимости между объемом промышленной продукции и инвестициями в основной капитал по рассматриваемым областям РФ.
Присвоим ранги признаку Y и фактору X. Найдем сумму разности квадратов d2.
Используя калькулятор, вычислим коэффициент ранговой корреляции Спирмена: ![]()
| X | Y | ранг X, dx | ранг Y, dy | (dx - dy)2 |
| 1.3 | 300 | 1 | 2 | 1 |
| 1.8 | 1335 | 2 | 12 | 100 |
| 2.4 | 250 | 3 | 1 | 4 |
| 3.4 | 946 | 4 | 8 | 16 |
| 4.8 | 670 | 5 | 7 | 4 |
| 5.1 | 400 | 6 | 4 | 4 |
| 6.3 | 380 | 7 | 3 | 16 |
| 7.5 | 450 | 8 | 5 | 9 |
| 7.8 | 500 | 9 | 6 | 9 |
| 17.5 | 1582 | 10 | 16 | 36 |
| 18.3 | 1216 | 11 | 9 | 4 |
| 22.5 | 1435 | 12 | 14 | 4 |
| 24.9 | 1445 | 13 | 15 | 4 |
| 25.8 | 1820 | 14 | 19 | 25 |
| 28.5 | 1246 | 15 | 10 | 25 |
| 33.4 | 1435 | 16 | 14 | 4 |
| 42.4 | 1800 | 17 | 18 | 1 |
| 45 | 1360 | 18 | 13 | 25 |
| 50.4 | 1256 | 19 | 11 | 64 |
| 54.8 | 1700 | 20 | 17 | 9 |
| 364 |
Связь между признаком Y фактором X сильная и прямая.
Оценка коэффициента ранговой корреляции Спирмена
Значимость коэффициента ранговой корреляции Спирмена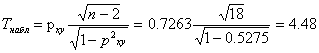
По таблице Стьюдента находим Tтабл.
Tтабл = (18;0.05) = 1.734
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве нулю коэффициента ранговой корреляции. Другими словами, коэффициента ранговой корреляции Спирмена статистически - значим.
Интервальная оценка для коэффициента ранговой корреляции (доверительный интервал)
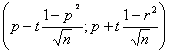
Доверительный интервал для коэффициента ранговой корреляции Спирмена: p(0.5431;0.9095).
Перейти к онлайн решению своего примера
Пример №2. Исходные данные.
| 5 | 4 |
| 3 | 4 |
| 1 | 3 |
| 3 | 1 |
| 6 | 6 |
| 2 | 2 |
| Номера мест в упорядоченном ряду | Расположение факторов по оценке эксперта | Новые ранги |
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 3 | 3.5 |
| 4 | 3 | 3.5 |
| 5 | 5 | 5 |
| 6 | 6 | 6 |
| Номера мест в упорядоченном ряду | Расположение факторов по оценке эксперта | Новые ранги |
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 3 | 3 |
| 4 | 4 | 4.5 |
| 5 | 4 | 4.5 |
| 6 | 6 | 6 |
| ранг X, dx | ранг Y, dy | (dx - dy)2 |
| 5 | 4.5 | 0.25 |
| 3.5 | 4.5 | 1 |
| 1 | 3 | 4 |
| 3.5 | 1 | 6.25 |
| 6 | 6 | 0 |
| 2 | 2 | 0 |
| 21 | 21 | 11.5 |
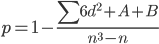
где
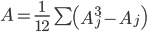
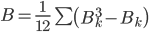
j - номера связок по порядку для признака х;
Аj - число одинаковых рангов в j-й связке по х;
k - номера связок по порядку для признака у;
Вk - число одинаковых рангов в k-й связке по у.
A = [(23-2)]/12 = 0.5
B = [(23-2)]/12 = 0.5
D = A + B = 0.5 + 0.5 = 1
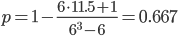
Связь между признаком Y и фактором X умеренная и прямая.
Задание №1. Определите тесноту связи с помощью коэффициента корреляции рангов Спирмена между X и Y.
Скачать решение
Задание №2. С помощью коэффициента ранговой корреляции Спирмена определите, между мнениями каких политических деятелей по вопросу приоритетов мероприятий региональной политики в России наблюдается наибольшее совпадение.
Пример №2
