Пример регрессионного анализа
Цели и задачи регрессионного анализа
Основная цель регрессионного анализа состоит в определении аналитической формы связи, в которой изменение результативного признака обусловлено влиянием одного или нескольких факторных признаков, а множество всех прочих факторов, также оказывающих влияние на результативный признак, принимается за постоянные и средние значения.Задачи регрессионного анализа:
а) Установление формы зависимости. Относительно характера и формы зависимости между явлениями, различают положительную линейную и нелинейную и отрицательную линейную и нелинейную регрессию.
б) Определение функции регрессии в виде математического уравнения того или иного типа и установление влияния объясняющих переменных на зависимую переменную.
в) Оценка неизвестных значений зависимой переменной. С помощью функции регрессии можно воспроизвести значения зависимой переменной внутри интервала заданных значений объясняющих переменных (т. е. решить задачу интерполяции) или оценить течение процесса вне заданного интервала (т. е. решить задачу экстраполяции). Результат представляет собой оценку значения зависимой переменной.
Парная регрессия - уравнение связи двух переменных у и х: y=f(x), где y - зависимая переменная (результативный признак); x - независимая, объясняющая переменная (признак-фактор).
Различают линейные и нелинейные регрессии.
Линейная регрессия: y = a + bx + ε
Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.
Регрессии, нелинейные по объясняющим переменным:
- полиномы разных степеней
y=a+b1·x+b2·x2+b3·x3+ε - равносторонняя гипербола
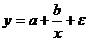 .
.
- степенная
y=a·xb·ε - показательная
y=a·bx·ε - экспоненциальная
y=ea+b·x·ε
Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно a и b:
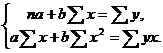
Можно воспользоваться готовыми формулами, которые вытекают из этой системы:
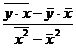
Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции rxy для линейной регрессии (-1≤rxy≤1):
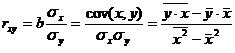
и индекс корреляции pxy - для нелинейной регрессии (0≤pxy≤1):
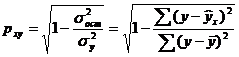
Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации.
Средняя ошибка аппроксимации - среднее отклонение расчетных значений от фактических:
Допустимый предел значений A - не более 8-10%.
Средний коэффициент эластичности Э показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на 1% от своего среднего значения:
Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:
∑(y-y)²=∑(yx-y)²+∑(y-yx)²
где ∑(y-y)² - общая сумма квадратов отклонений;
∑(yx-y)² - сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);
∑(y-yx)² - остаточная сумма квадратов отклонений.
Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент (индекс) детерминации R2:
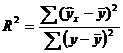
Коэффициент детерминации - квадрат коэффициента или индекса корреляции.
F-тест - оценивание качества уравнения регрессии - состоит в проверке гипотезы Но о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера. Fфакт определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
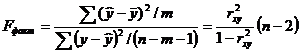 ,
,
где n - число единиц совокупности; m - число параметров при переменных х.
Fтабл - это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости a. Уровень значимости a - вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно a принимается равной 0,05 или 0,01.
Если Fтабл < Fфакт, то Но - гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если Fтабл > Fфакт, то гипотеза Но не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Но о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:
![]() ;
; ![]() ;
; ![]() .
.
Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:
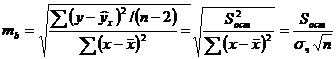
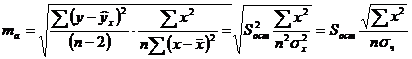
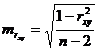
Сравнивая фактическое и критическое (табличное) значения t-статистики - tтабл и tфакт - принимаем или отвергаем гипотезу Но.
Связь между F-критерием Фишера и t-статистикой Стьюдента выражается равенством
Если tтабл < tфакт то Ho отклоняется, т.е. a, b и rxy не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х. Если tтабл > tфакт то гипотеза Но не отклоняется и признается случайная природа формирования а, b или rxy.
Для расчета доверительного интервала определяем предельную ошибку D для каждого показателя:
Δa=tтабл·ma, Δb=tтабл·mb.
Формулы для расчета доверительных интервалов имеют следующий вид:
γa=a±Δa; γa=a-Δa; γa=a+Δa
γb=b±Δb; γb=b-Δb; γb=b+Δb
Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.
Прогнозное значение yp определяется путем подстановки в уравнение регрессии yx=a+b·x соответствующего (прогнозного) значения xp. Вычисляется средняя стандартная ошибка прогноза myx:
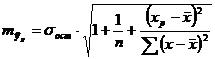 ,
,
где
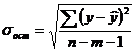
и строится доверительный интервал прогноза:
γyx=yp±Δyp; γyxmin=yp-Δyp; γyxmax=yp+Δyp
где Δyx=tтабл·myx.
Пример решения
Задача №1. По семи территориям Уральского района За 199Х г. известны значения двух признаков.Таблица 1.
| Район | Расходы на покупку продовольственных товаров в общих расходах, %, у | Среднедневная заработная плата одного работающего, руб., х |
| Удмуртская респ. | 68,8 + N/2 | 45,1 – K/2 |
| Свердловская обл. | 61,2 + M/2 | 59,0 – N/2 |
| Башкортостан | 59,9 + K/2 | 57,2 – M/2 |
| Челябинская обл. | 56,7 + N/2 | 61,8 – K/2 |
| Пермская обл. | 55,0 + K/2 | 58,8 – N/2 |
| Курганская обл. | 54,3 + M/2 | 47,2 – K/2 |
| Оренбургская обл. | 49,3 + K/2 | 55,2 – M/2 |
Требуется: 1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
а) линейной;
б) степенной (предварительно нужно произвести процедуру линеаризации переменных, путем логарифмирования обеих частей);
в) показательной;
г) равносторонней гиперболы (так же нужно придумать как предварительно линеаризовать данную модель).
2. Оценить каждую модель через среднюю ошибку аппроксимации A и F-критерий Фишера.
Решение (Вариант №1)
Для расчета параметров a и b линейной регрессии y=a+b·x (расчет можно проводить с помощью калькулятора).решаем систему нормальных уравнений относительно а и b:
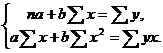
По исходным данным рассчитываем ∑y, ∑x, ∑y·x, ∑x², ∑y²:
| y | x | yx | x2 | y2 | yx | y-yx | Ai | |
| l | 68,8 | 45,1 | 3102,88 | 2034,01 | 4733,44 | 61,3 | 7,5 | 10,9 |
| 2 | 61,2 | 59,0 | 3610,80 | 3481,00 | 3745,44 | 56,5 | 4,7 | 7,7 |
| 3 | 59,9 | 57,2 | 3426,28 | 3271,84 | 3588,01 | 57,1 | 2,8 | 4,7 |
| 4 | 56,7 | 61,8 | 3504,06 | 3819,24 | 3214,89 | 55,5 | 1,2 | 2,1 |
| 5 | 55,0 | 58,8 | 3234,00 | 3457,44 | 3025,00 | 56,5 | -1,5 | 2,7 |
| 6 | 54,3 | 47,2 | 2562,96 | 2227,84 | 2948,49 | 60,5 | -6,2 | 11,4 |
| 7 | 49,3 | 55,2 | 2721,36 | 3047,04 | 2430,49 | 57,8 | -8,5 | 17,2 |
| Итого | 405,2 | 384,3 | 22162,34 | 21338,41 | 23685,76 | 405,2 | 0,0 | 56,7 |
| Ср. знач. (Итого/n) | 57,89 y | 54,90 x | 3166,05 x·y | 3048,34 x² | 3383,68 y² | X | X | 8,1 |
| s | 5,74 | 5,86 | X | X | X | X | X | X |
| s2 | 32,92 | 34,34 | X | X | X | X | X | X |
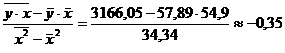
a=y-b·x = 57.89+0.35·54.9 ≈ 76.88
Уравнение регрессии: у = 76,88 - 0,35х. С увеличением среднедневной заработной платы на 1 руб. доля расходов на покупку продовольственных товаров снижается в среднем на 0,35 %-ных пункта.
Рассчитаем линейный коэффициент парной корреляции:
![]()
Связь умеренная, обратная.
Определим коэффициент детерминации: r²xy=(-0.35)=0.127
Вариация результата на 12,7% объясняется вариацией фактора х. Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения yx. Найдем величину средней ошибки аппроксимации A:
![]()
В среднем расчетные значения отклоняются от фактических на 8,1%.
Рассчитаем F-критерий:
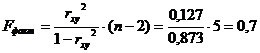
Полученное значение указывает на необходимость принять гипотезу Н0 о случайной природе выявленной зависимости и статистической незначимости параметров уравнения и показателя тесноты связи.
1б. Построению степенной модели y=a·xb предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
lg y=lg a + b·lg x
Y=C+b·Y
где Y=lg(y), X=lg(x), C=lg(a).
Для расчетов используем данные табл. 1.3.
Таблица 1.3
| Y | X
| YX
| Y2
| X2 | yx | y-yx | (y-yx)² | Ai | |
| 1 | 1,8376 | 1,6542 | 3,0398 | 3,3768 | 2,7364 | 61,0 | 7,8 | 60,8 | 11,3 |
| 2 | 1,7868 | 1,7709 | 3,1642 | 3,1927 | 3,1361 | 56,3 | 4,9 | 24,0 | 8,0 |
| 3 | 1,7774 | 1,7574 | 3,1236 | 3,1592 | 3,0885 | 56,8 | 3,1 | 9,6 | 5,2 |
| 4 | 1,7536 | 1,7910 | 3,1407 | 3,0751 | 3,2077 | 55,5 | 1,2 | 1,4 | 2,1 |
| 5 | 1,7404 | 1,7694 | 3,0795 | 3,0290 | 3,1308 | 56,3 | -1,3 | 1,7 | 2,4 |
| 6 | 1,7348 | 1,6739 | 2,9039 | 3,0095 | 2,8019 | 60,2 | -5,9 | 34,8 | 10,9 |
| 7 | 1,6928 | 1,7419 | 2,9487 | 2,8656 | 3,0342 | 57,4 | -8,1 | 65,6 | 16,4 |
| Итого | 12,3234 | 12,1587 | 21,4003 | 21,7078 | 21,1355 | 403,5 | 1,7 | 197,9 | 56,3 |
| Среднее значение | 1,7605 | 1,7370 | 3,0572 | 3,1011 | 3,0194 | X | X | 28,27 | 8,0 |
| σ | 0,0425 | 0,0484 | X | X | X | X | X | X | X |
| σ2 | 0,0018 | 0,0023 | X | X | X | X | X | X | X |
Рассчитаем С и b:
![]()
C=Y-b·X = 1.7605+0.298·1.7370 = 2.278126
Получим линейное уравнение: Y=2.278-0.298·X
Выполнив его потенцирование, получим: y=102.278·x-0.298
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата![]() . По ним рассчитаем показатели: тесноты связи - индекс корреляции pxy и среднюю ошибку аппроксимации A.
. По ним рассчитаем показатели: тесноты связи - индекс корреляции pxy и среднюю ошибку аппроксимации A.
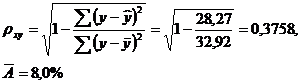
Характеристики степенной модели указывают, что она несколько лучше линейной функции описывает взаимосвязь.
1в. Построению уравнения показательной кривой y=a·bx предшествует процедура линеаризации переменных при логарифмировании обеих частей уравнения:
lg y=lg a + x·lg b
Y=C+B·x
Для расчетов используем данные таблицы.
Таблица
| Y | x | Yx | Y2 | x2 | yx | y-yx | (y-yx)² | Ai | |
| 1 | 1,8376 | 45,1 | 82,8758 | 3,3768 | 2034,01 | 60,7 | 8,1 | 65,61 | 11,8 |
| 2 | 1,7868 | 59,0 | 105,4212 | 3,1927 | 3481,00 | 56,4 | 4,8 | 23,04 | 7,8 |
| 3 | 1,7774 | 57,2 | 101,6673 | 3,1592 | 3271,84 | 56,9 | 3,0 | 9,00 | 5,0 |
| 4 | 1,7536 | 61,8 | 108,3725 | 3,0751 | 3819,24 | 55,5 | 1,2 | 1,44 | 2,1 |
| 5 | 1,7404 | 58,8 | 102,3355 | 3,0290 | 3457,44 | 56,4 | -1,4 | 1,96 | 2,5 |
| 6 | 1,7348 | 47,2 | 81,8826 | 3,0095 | 2227,84 | 60,0 | -5,7 | 32,49 | 10,5 |
| 7 | 1,6928 | 55,2 | 93,4426 | 2,8656 | 3047,04 | 57,5 | -8,2 | 67,24 | 16,6 |
| Итого | 12,3234 | 384,3 | 675,9974 | 21,7078 | 21338,41 | 403,4 | -1,8 | 200,78 | 56,3 |
| Ср. зн. | 1,7605 | 54,9 | 96,5711 | 3,1011 | 3048,34 | X | X | 28,68 | 8,0 |
| σ | 0,0425 | 5,86 | X | X | X | X | X | X | X |
| σ2 | 0,0018 | 34,339 | X | X | X | X | X | X | X |
Значения параметров регрессии A и В составили:
![]()
A=Y-B·x = 1.7605+0.0023·54.9 = 1.887
Получено линейное уравнение: Y=1.887-0.0023x. Произведем потенцирование полученного уравнения и запишем его в обычной форме:
yx=101.887·10-0.0023x = 77.1·0.9947x
Тесноту связи оценим через индекс корреляции pxy:
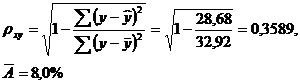
Связь умеренная.
A=8,0%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах. Показательная функция чуть хуже, чем степенная, описывает изучаемую зависимость.
1г. Уравнение равносторонней гиперболы ![]() линеаризуется при замене:
линеаризуется при замене:![]() . Тогда y=a+b·z. Для расчетов используем данные таблицы.
. Тогда y=a+b·z. Для расчетов используем данные таблицы.
| y | z | yz | z2 | y2 | yx | y-yx | (y-yx)² | Ai | |
| 1 | 68,8 | 0,0222 | 1,5255 | 0,000492 | 4733,44 | 61,8 | 7,0 | 49,00 | 10,2 |
| 2 | 61,2 | 0,0169 | 1,0373 | 0,000287 | 3745,44 | 56,3 | 4,9 | 24,01 | 8,0 |
| 3 | 59,9 | 0,0175 | 1,0472 | 0,000306 | 3588,01 | 56,9 | 3,0 | 9,00 | 5,0 |
| 4 | 56,7 | 0,0162 | 0,9175 | 0,000262 | 3214,89 | 55,5 | 1,2 | 1,44 | 2,1 |
| 5 | 55 | 0,0170 | 0,9354 | 0,000289 | 3025,00 | 56,4 | -1,4 | 1,96 | 2,5 |
| 6 | 54,3 | 0,0212 | 1,1504 | 0,000449 | 2948,49 | 60,8 | -6,5 | 42,25 | 12,0 |
| 7 | 49,3 | 0,0181 | 0,8931 | 0,000328 | 2430,49 | 57,5 | -8,2 | 67,24 | 16,6 |
| Итого | 405,2 | 0,1291 | 7,5064 | 0,002413 | 23685,76 | 405,2 | 0,0 | 194,90 | 56,5 |
| Среднее значение | 57,9 | 0,0184 | 1,0723 | 0,000345 | 3383,68 | X | X | 27,84 | 8,1 |
| σ | 5,74 | 0,002145 | X | X | X | X | X | X | X |
| σ2 | 32,9476 | 0,000005 | X | X | X | X | X | X | X |
Значения параметров регрессии а и b составили:
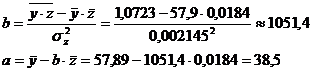
Получено уравнение: ![]()
Индекс корреляции: 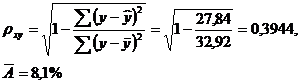
По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи: pyxy=0.3944 (по сравнению с линейной, степенной и показательной регрессиями). A остается на допустимом уровне: 8,1%.
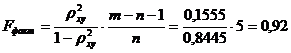
где Fтабл= 6,6 > Fфакт, при α =0,05.
Следовательно, принимается гипотеза Н0 о статистически незначимых параметрах этого уравнения. Этот результат можно объяснить сравнительно невысокой теснотой выявленной зависимости и небольшим числом наблюдений.
