Критерий Стьюдента
t-статистика предназначена для определения статистической значимости каждого коэффициента уравнения. Для установления сходства или различия средних арифметических значений в двух выборках используйте этот t-критерий.Рассмотрим пример решения стандартной задачи. Целью расчетов является ответ на вопрос, являются ли полученные коэффициенты регрессии a и b статистически значимыми? Другими словами, отличны ли они от нуля и существенно ли влияют на результативный признак?
Будем исследовать зависимость размера дивидендов Y акций группы компаний от доходности акций X.
Линейное уравнение регрессии имеет вид y = bx + a + ε
Система нормальных уравнений.
a•n + b∑x = ∑y
a∑x + b∑x2 = ∑y•x
Для наших данных система уравнений имеет вид
50a + 343.53 b = 1679.25
343.53 a + 2510.58 b = 11912.45
Из первого уравнения выражаем а и подставим во второе уравнение:
Получаем эмпирические коэффициенты регрессии: b = 2.4948, a = 16.4443
Уравнение регрессии (эмпирическое уравнение регрессии):
y = 2.4948 x + 16.4443
Для расчета параметров регрессии построим расчетную таблицу (табл. 1)
| x | y | x2 | y2 | x • y |
| 8.19 | 42.08 | 67.14 | 1770.46 | 344.77 |
| 7.65 | 36.51 | 58.53 | 1333.01 | 279.32 |
| 4.56 | 23.76 | 20.76 | 564.4 | 108.24 |
| 5.92 | 27.23 | 35.02 | 741.68 | 161.17 |
| 8.15 | 25.44 | 66.45 | 647.33 | 207.41 |
| 6.51 | 35.44 | 42.37 | 1256.17 | 230.71 |
| 6.23 | 34.18 | 38.82 | 1168.53 | 212.99 |
| 6.42 | 27.33 | 41.27 | 747.19 | 175.6 |
| 6.9 | 32.69 | 47.55 | 1068.57 | 225.42 |
| 7.45 | 34.74 | 55.55 | 1207.12 | 258.96 |
| 7.58 | 32.47 | 57.38 | 1054.09 | 245.94 |
| 6.6 | 30.18 | 43.61 | 910.77 | 199.29 |
| 3.28 | 28.01 | 10.77 | 784.56 | 91.91 |
| 7.42 | 39.48 | 54.99 | 1558.45 | 292.74 |
| 8.91 | 47.81 | 79.32 | 2285.38 | 425.77 |
| 8.42 | 45.7 | 70.87 | 2088.63 | 384.74 |
| 6.11 | 29.39 | 37.39 | 864.01 | 179.73 |
| 9.48 | 38.19 | 89.96 | 1458.76 | 362.25 |
| 8.97 | 30.78 | 80.43 | 947.36 | 276.03 |
| 5.79 | 37.86 | 33.48 | 1433.68 | 219.09 |
| 4.77 | 24.29 | 22.77 | 590.16 | 115.92 |
| 7.79 | 37.28 | 60.64 | 1389.55 | 290.29 |
| 6.99 | 27.78 | 48.89 | 771.49 | 194.21 |
| 4.43 | 31.61 | 19.6 | 999.26 | 139.95 |
| 6.04 | 31.09 | 36.5 | 966.62 | 187.84 |
| 8.84 | 40.95 | 78.14 | 1677.22 | 362.02 |
| 8.06 | 41.38 | 64.93 | 1712.12 | 333.41 |
| 8.57 | 45.16 | 73.42 | 2039.53 | 386.98 |
| 4.78 | 21.62 | 22.83 | 467.5 | 103.3 |
| 7.01 | 39.76 | 49.12 | 1581.1 | 278.67 |
| 3.25 | 24.2 | 10.57 | 585.61 | 78.67 |
| 6.41 | 32.4 | 41.05 | 1050.04 | 207.6 |
| 6.91 | 29.79 | 47.8 | 887.69 | 206 |
| 5.84 | 35.63 | 34.14 | 1269.63 | 208.2 |
| 6.38 | 32.35 | 40.75 | 1046.49 | 206.49 |
| 8.37 | 37.57 | 70 | 1411.56 | 314.34 |
| 8.02 | 34.01 | 64.33 | 1156.46 | 272.74 |
| 11.7 | 43.06 | 136.92 | 1853.84 | 503.82 |
| 5.92 | 38.63 | 35.05 | 1492.23 | 228.71 |
| 7.69 | 34.49 | 59.18 | 1189.37 | 265.3 |
| 9.32 | 35.13 | 86.86 | 1233.89 | 327.37 |
| 8.63 | 37.22 | 74.46 | 1385.56 | 321.21 |
| 6.14 | 27.77 | 37.68 | 771.31 | 170.49 |
| 8.22 | 39.84 | 67.55 | 1587.14 | 327.43 |
| 6.2 | 34.03 | 38.5 | 1158.06 | 211.15 |
| 2.35 | 22.38 | 5.55 | 501.04 | 52.71 |
| 5.34 | 30.51 | 28.48 | 930.89 | 162.82 |
| 6.36 | 33.92 | 40.47 | 1150.52 | 215.78 |
| 5.16 | 27.16 | 26.63 | 737.7 | 140.16 |
| 7.49 | 28.94 | 56.12 | 837.46 | 216.78 |
| 343.53 | 1679.25 | 2510.58 | 58321.22 | 11912.45 |
Параметры уравнения регрессии.
Выборочные средние.
Выборочные дисперсии:
Среднеквадратическое отклонение
Для оценки качества параметров регрессии построим расчетную таблицу (табл. 2)
| x | y | y(x) | (yi-ycp)2 | (y-y(x))2 |
| 8.19 | 42.08 | 36.89 | 72.11 | 26.94 |
| 7.65 | 36.51 | 35.53 | 8.56 | 0.96 |
| 4.56 | 23.76 | 27.81 | 96.58 | 16.43 |
| 5.92 | 27.23 | 31.21 | 40.34 | 15.8 |
| 8.15 | 25.44 | 36.78 | 66.29 | 128.57 |
| 6.51 | 35.44 | 32.68 | 3.45 | 7.61 |
| 6.23 | 34.18 | 31.99 | 0.36 | 4.82 |
| 6.42 | 27.33 | 32.47 | 39.06 | 26.38 |
| 6.9 | 32.69 | 33.65 | 0.8 | 0.92 |
| 7.45 | 34.74 | 35.04 | 1.34 | 0.0871 |
| 7.58 | 32.47 | 35.34 | 1.25 | 8.27 |
| 6.6 | 30.18 | 32.92 | 11.6 | 7.51 |
| 3.28 | 28.01 | 24.63 | 31.08 | 11.42 |
| 7.42 | 39.48 | 34.94 | 34.72 | 20.55 |
| 8.91 | 47.81 | 38.66 | 202.23 | 83.57 |
| 8.42 | 45.7 | 37.45 | 146.81 | 68.14 |
| 6.11 | 29.39 | 31.7 | 17.56 | 5.31 |
| 9.48 | 38.19 | 40.11 | 21.24 | 3.66 |
| 8.97 | 30.78 | 38.82 | 7.87 | 64.62 |
| 5.79 | 37.86 | 30.88 | 18.31 | 48.78 |
| 4.77 | 24.29 | 28.35 | 86.34 | 16.45 |
| 7.79 | 37.28 | 35.87 | 13.63 | 1.97 |
| 6.99 | 27.78 | 33.89 | 33.75 | 37.36 |
| 4.43 | 31.61 | 27.49 | 3.9 | 16.99 |
| 6.04 | 31.09 | 31.52 | 6.22 | 0.18 |
| 8.84 | 40.95 | 38.5 | 54.3 | 6.03 |
| 8.06 | 41.38 | 36.55 | 60.73 | 23.34 |
| 8.57 | 45.16 | 37.82 | 134.01 | 53.87 |
| 4.78 | 21.62 | 28.36 | 143.12 | 45.45 |
| 7.01 | 39.76 | 33.93 | 38.17 | 34.04 |
| 3.25 | 24.2 | 24.55 | 88.09 | 0.13 |
| 6.41 | 32.4 | 32.43 | 1.39 | 0.000554 |
| 6.91 | 29.79 | 33.69 | 14.37 | 15.21 |
| 5.84 | 35.63 | 31.02 | 4.19 | 21.25 |
| 6.38 | 32.35 | 32.37 | 1.53 | 0.000389 |
| 8.37 | 37.57 | 37.32 | 15.89 | 0.0643 |
| 8.02 | 34.01 | 36.45 | 0.18 | 5.99 |
| 11.7 | 43.06 | 45.64 | 89.71 | 6.66 |
| 5.92 | 38.63 | 31.22 | 25.45 | 54.97 |
| 7.69 | 34.49 | 35.64 | 0.81 | 1.32 |
| 9.32 | 35.13 | 39.7 | 2.38 | 20.87 |
| 8.63 | 37.22 | 37.97 | 13.24 | 0.56 |
| 6.14 | 27.77 | 31.76 | 33.78 | 15.9 |
| 8.22 | 39.84 | 36.95 | 39.11 | 8.35 |
| 6.2 | 34.03 | 31.92 | 0.2 | 4.44 |
| 2.35 | 22.38 | 22.32 | 125.46 | 0.00418 |
| 5.34 | 30.51 | 29.76 | 9.45 | 0.57 |
| 6.36 | 33.92 | 32.32 | 0.11 | 2.57 |
| 5.16 | 27.16 | 29.32 | 41.27 | 4.66 |
| 7.49 | 28.94 | 35.13 | 21.59 | 38.37 |
| 343.53 | 1679.25 | 1679.25 | 1923.93 | 987.9 |
2. Оценка параметров уравнения регрессии.
2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:
S2y = 20.58 - необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).
Sy = 4.54 - стандартная ошибка оценки (стандартная ошибка регрессии).
Sa - стандартное отклонение случайной величины a.
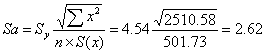
Sb - стандартное отклонение случайной величины b.
Перейти к онлайн решению своей задачи
Оценим значимость показателей уравнения регрессии, которое наиболее адекватно описывает зависимость между показателями с вероятностью 95%.
С помощью МНК мы получили лишь оценки параметров уравнения регрессии, которые характерны для конкретного статистического наблюдения (конкретного набора значений x и y).
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Н0 о случайной природе показателей, т.е. о незначимом их отличии от нуля.
Чтобы проверить, значимы ли параметры, т.е. значимо ли они отличаются от нуля для генеральной совокупности используют статистические методы проверки гипотез.
В качестве основной (нулевой) гипотезы выдвигают гипотезу о незначимом отличии от нуля параметра или статистической характеристики в генеральной совокупности. Наряду с основной (проверяемой) гипотезой выдвигают альтернативную (конкурирующую) гипотезу о неравенстве нулю параметра или статистической характеристики в генеральной совокупности.
Проверим гипотезу H0 о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H1 не равно) на уровне значимости α=0.05.
В случае, если основная гипотеза окажется неверной, мы принимаем альтернативную. Для проверки этой гипотезы используется t-критерий Стьюдента.
Найденное по данным наблюдений значение t-критерия (его еще называют наблюдаемым или фактическим) сравнивается с табличным (критическим) значением, определяемым по таблицам распределения Стьюдента (которые обычно приводятся в конце учебников и практикумов по статистике или эконометрике).
Табличное значение определяется в зависимости от уровня значимости (α) и числа степеней свободы, которое в случае линейной парной регрессии равно (n-2), n-число наблюдений. Таким образом, Табличное значение t-статистика зависит и от доверительной вероятности, и от числа факторов и от длины исходного ряда.
Если фактическое значение t-критерия больше табличного (по модулю), то основную гипотезу отвергают и считают, что с вероятностью (1-α) параметр или статистическая характеристика в генеральной совокупности значимо отличается от нуля.
Если фактическое значение t-критерия меньше табличного (по модулю), то нет оснований отвергать основную гипотезу, т.е. параметр или статистическая характеристика в генеральной совокупности незначимо отличается от нуля при уровне значимости α.
tкрит (n-m-1;α/2) = (48;0.025) = 2.009
![]()
Поскольку 6.74 > 2.009, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
![]()
Поскольку 6.27 > 2.009, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Вывод: Полученные коэффициенты регрессии a и b - статистически значимы, и поэтому их можно использовать в уравнении линейной регрессии для дальнейших анализов и прогнозов.
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:(b - tкрит Sb; b + tкрит Sb)
(2.49 - 2.009 • 0.37; 2.49 + 2.009 • 0.37)
(1.75;3.24)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
(a - tкрит Sa; a + tкрит Sa)
(16.44 - 2.009 • 2.62; 16.44 + 2.009 • 2.62)
(11.18;21.71)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
см. также Как оценить уравнение регрессии в целом? (проверка гипотезы о том, что коэффициенты регрессии одновременно равны нулю, a=0, b=0)

