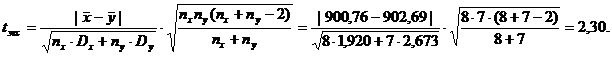Проверка статистических гипотез
Назначение сервиса. С помощью онлайн-калькулятора осуществляется:- проверка гипотезы о равенстве дисперсий, t-критерий Фишера;
- проверка гипотезы о равенстве генеральных средних (математических ожиданий), t-критерий Стьюдента;
- проверка равенства дисперсий по критерию Кохрена.
- см. примеры.
Пример №2. По двум независимым малым выборкам, объемы которых 12 и 18, извлеченным из нормальных генеральных совокупностей X и Y, найдены x и y и дисперсии D(X) и D(Y). Требуется при уровне значимости γ=0,05 проверить нулевую гипотезу H0: M(X)=M(Y) при конкурирующей гипотезе H1: M(X)≠M(Y)
Проверка гипотезы о значении дисперсии генеральной совокупности
Гипотеза о равенстве двух дисперсий нормально распределённых генеральных совокупностей.
В данном случае при уровне значимости α нужно проверить гипотезу Н0: D(Х) = D(Y). Статистикой служит случайная величина 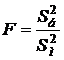 , имеющая распределение Фишера – Снедекора с f1 = nб – 1 и f2 = nм – 1 степенями свободы (S2б – большая дисперсия (максимальная из двух), объём её выборки nб). Определяется соответствующее экспериментальное (наблюдаемое) значение Fэкс. Критическое значение Fкр при альтернативной гипотезе Н1: D(Х) > D(Y) находится из таблицы критических точек распределения Фишера – Снедекора по уровню значимости α и числу степеней свободы f1 и f2. Нулевая гипотеза принимается, если Fэкс < Fкр.
, имеющая распределение Фишера – Снедекора с f1 = nб – 1 и f2 = nм – 1 степенями свободы (S2б – большая дисперсия (максимальная из двух), объём её выборки nб). Определяется соответствующее экспериментальное (наблюдаемое) значение Fэкс. Критическое значение Fкр при альтернативной гипотезе Н1: D(Х) > D(Y) находится из таблицы критических точек распределения Фишера – Снедекора по уровню значимости α и числу степеней свободы f1 и f2. Нулевая гипотеза принимается, если Fэкс < Fкр.
Пример. Из первого нарезного оружия было произведено 8 выстрелов. При этом измерялись начальные скорости пуль. Получены следующие результаты: 902,4;901,3;898,4;903,5;901,1; 900,4;899,7; 900,3 (м/с). Из второго оружия было произведено 7 выстрелов. Скорости вылета пуль оказались равны 905,5; 910,3;903,8;902,4; 899,9;903,3; 905,6 (м/с).
Для обеих выборок вычислите среднее, исправленную дисперсию и среднее квадратическое отклонение. Найдите размах варьирования, среднее абсолютное (линейное) отклонение, коэффициент вариации, линейный коэффициент вариации, коэффициент осцилляции.
Предполагая, что данная случайная величина имеет нормальное распределение, определите доверительный интервал для генеральной средней (в обоих случаях).
По критерию Фишера проверьте гипотезу о равенстве генеральных дисперсий. По критерию Стьюдента проверьте гипотезу о равенстве генеральных средних (альтернативная гипотеза – об их неравенстве).
Во всех расчётах уровень значимости α = 0,05.
Решение. По формулам для первого оружия вычислим среднее значение, исправленную дисперсию и исправленное среднее квадратическое отклонение:
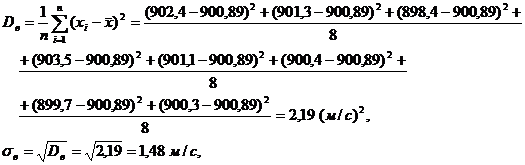
Используя калькулятор, находим для первого оружия другие характеристики вариации:
- размах варьирования R = xmax – xmin = 903,5 – 898,4 = 5,1;
- среднее абсолютное (линейное) отклонение
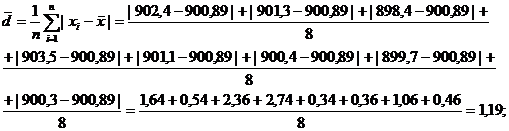
- коэффициент вариации
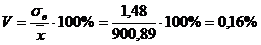 ;
;
- линейный коэффициент вариации
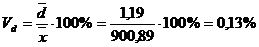 ;
;
- коэффициент осцилляции
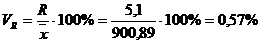 .
.
Для доверительной вероятности γ = 0,95 (уровень значимости α = 0,05) по таблице критических точек распределения Стьюдента при f = 8 – 1 = 7 степенях свободы находим значение коэффициента tg = 2,36. Тогда полуширина доверительного интервала
![]() .
.
И с вероятностью g = 0,95 генеральное среднее начальной скорости пули лежит в интервале (900,89 ± 1,32) м/с или (899,57; 902,21) м/с.
Повторим все расчёты для второго оружия:
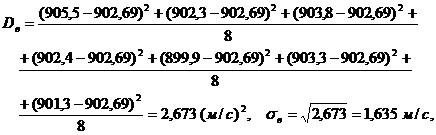
R = ymax – ymin = 905,5 – 899,9 = 5,6;
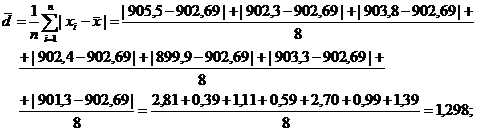
Для доверительной вероятности g= 0,95 (уровень значимости a = 0,05) по таблице критических точек распределения Стьюдента при f = 7 – 1 = 6 степенях свободы находим значение коэффициента tg = 2,45. Тогда полуширина доверительного интервала
![]() .
.
И с вероятностью γ = 0,95 генеральное среднее начальной скорости пули лежит в интервале (902,69 ± 1,63) м/с или (901,03; 904,32) м/с.
Проводим проверку гипотезы о равенстве дисперсий:
H0: Dx = Dy;
H1: Dx < Dy.
Найдём наблюдаемое значение критерия Фишера ![]() .
.
f1 = nб – 1 = nу – 1 = 7 – 1 = 6 и f2 = nм – 1 = nх – 1 = 8 – 1 = 7 (числа степеней свободы). По таблице критических точек распределения Фишера – Снедекора при уровне значимости α = 0,05 и данным числам степеней свободы находим Fкр = 3,87. Т.к. Fэкс < Fкр, то нет оснований отвергать нулевую гипотезу (т.е. можно считать, что дисперсии двух выборок равны).
Проводим проверку гипотезы о равенстве генеральных средних:
H0: x=y;
H1: x≠y.
Найдём экспериментальное значение критерия Стьюдента