Однофакторный дисперсионный анализ
Дисперсионный анализ представляет собой систему понятий и технических приемов, позволяющих обобщить процедуру сравнения двух средних для двух выборок, взятых из генеральных совокупностей с нормальным распределением, на случай большого числа выборок.Назначение сервиса. С помощью данного онлайн-калькулятора можно:
- провести однофакторный дисперсионный анализ;
- ответить на вопрос - совпадают или нет средние значения экспериментов;
- при выбранном уровне значимости подтвердить или опровергнуть нулевую гипотезу H0 о равенстве групповых средних;
см. также Двухфакторный дисперсионный анализ, Проверка статистических гипотез
Пример. Изделие железнодорожного транспорта с целью испытания на надежность эксплуатируется q раз, i=1,...q на p уровнях времени работы Tj , j=1,..., p. В каждом испытании подсчитываются числа отказов nij. На уровне значимости α = 0,05 исследовать влияние времени работы изделия на число появления отказов методом однофакторного дисперсионного анализа при q=4, p=4. Результаты испытаний nij представлены в таблицах.
Решение.
Процедура однофакторного дисперсионного анализа. Находим групповые средние:
![]()
| N | П1 | П2 | П3 | П4 |
| 1 | 145 | 210 | 195 | 155 |
| 2 | 140 | 200 | 190 | 150 |
| 3 | 150 | 190 | 240 | 180 |
| 4 | 190 | 195 | 210 | 175 |
| x | 156.25 | 198.75 | 208.75 | 165 |
Обозначим р - количество уровней фактора (р=4). Число измерений на каждом уровне одинаково и равно q=4.
В последней строке помещены групповые средние для каждого уровня фактора.
Общую среднюю можно получить как среднее арифметическое групповых средних:
На разброс групповых средних процента отказа относительно общей средней влияют как изменения уровня рассматриваемого фактора, так и случайные факторы.
Для того чтобы учесть влияние данного фактора, общая выборочная дисперсия разбивается на две части, первая из которых называется факторной S2ф, а вторая - остаточной S2ост.
С целью учета этих составляющих вначале рассчитывается общая сумма квадратов отклонений вариант от общей средней:
Rобщ = ∑∑(xij-x) (2)
и факторная сумма квадратов отклонений групповых средних от общей средней, которая и характеризует влияние данного фактора:
Rф = q·(xij-x)
Последнее выражение получено путем замены каждой варианты в выражении Rобщ групповой средней для данного фактора.
Остаточная сумма квадратов отклонений получается как разность:
Rост = Rобщ - Rф
Для определения общей выборочной дисперсии необходимо Rобщ разделить на число измерений pq:
а для получения несмещенной общей выборочной дисперсии это выражение нужно умножить на pq/(pq-1):
Соответственно, для несмещенной факторной выборочной дисперсии:
где p-1 - число степеней свободы несмещенной факторной выборочной дисперсии.
С целью оценки влияния фактора на изменения рассматриваемого параметра рассчитывается величина:
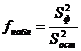
Так как отношение двух выборочных дисперсий S2ф и S2ост распределено по закону Фишера-Снедекора, то полученное значение fнабл сравнивают со значением функции распределения
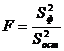
в критической точке fкр, соответствующей выбранному уровню значимости a.
Если fнабл>fкр, то фактор оказывает существенное воздействие и его следует учитывать, в противном случае он оказывает незначительное влияние, которым можно пренебречь.
Для расчета Rнабл и Rф могут быть использованы также формулы:
Находим общую среднюю по формуле (1):
Для расчета Rобщ по формуле (4) составляем таблицу 2 квадратов вариант:
| N | П21 | П22 | П23 | П24 |
| 1 | 21025 | 44100 | 38025 | 24025 |
| 2 | 19600 | 40000 | 36100 | 22500 |
| 3 | 22500 | 36100 | 57600 | 32400 |
| 4 | 36100 | 38025 | 44100 | 30625 |
| ∑ | 99225 | 158225 | 175825 | 109550 |
Общая средняя вычисляется по формуле (1):
Rобщ = 99225 + 158225 + 175825 + 109550 - 4 • 4 • 182.192 = 11748.44
Находим Rф по формуле (5):
Rф = 4(156.252 + 198.752 + 208.752 + 1652) - 4 • 182.192 = 7792.19
Получаем Rост: Rост = Rобщ - Rф = 11748.44 - 7792.19 = 3956.25
Определяем факторную и остаточную дисперсии:
Если средние значения случайной величины, вычисленные по отдельным выборкам одинаковы, то оценки факторной и остаточной дисперсий являются несмещенными оценками генеральной дисперсии и различаются несущественно.
Тогда сопоставление оценок этих дисперсий по критерию Фишера должно показать, что нулевую гипотезу о равенстве факторной и остаточной дисперсий отвергнуть нет оснований.
Оценка факторной дисперсии больше оценки остаточной дисперсии, поэтому можно сразу утверждать не справедливость нулевой гипотезы о равенстве математических ожиданий по слоям выборки.
Иначе говоря, в данном примере фактор Ф оказывает существенное влияния на случайную величину.
Проверим нулевую гипотезу H0: равенство средних значений х.
Находим fнабл ![]()
Для уровня значимости α=0.05, чисел степеней свободы 3 и 12 находим fкр из таблицы распределения Фишера-Снедекора.
fкр(0.05; 3; 12) = 3.49
В связи с тем, что fнабл > fкр, нулевую гипотезу о существенном влиянии фактора на результаты экспериментов принимаем.
Пример №2. Студентов 1-го курса опрашивали с целью выявления занятий, которым они посвящают свое свободное время. Проверьте, различаются ли распределение вербальных и невербальных предпочтений студентов.
Находим групповые средние:
![]()
| N | П1 | П2 |
| 1 | 12 | 17 |
| 2 | 18 | 19 |
| 3 | 23 | 25 |
| 4 | 10 | 7 |
| 5 | 15 | 17 |
| x | 15.6 | 17 |
В последней строке помещены групповые средние для каждого уровня фактора.
Общую среднюю можно получить как среднее арифметическое групповых средних:
На разброс групповых средних процента отказа относительно общей средней влияют как изменения уровня рассматриваемого фактора, так и случайные факторы.
Для того чтобы учесть влияние данного фактора, общая выборочная дисперсия разбивается на две части, первая из которых называется факторной S2ф, а вторая - остаточной S2ост.
С целью учета этих составляющих вначале рассчитывается общая сумма квадратов отклонений вариант от общей средней:
Rобщ=∑∑(xij-x)
и факторная сумма квадратов отклонений групповых средних от общей средней, которая и характеризует влияние данного фактора:
Rф=q∑(xij-x)
Последнее выражение получено путем замены каждой варианты в выражении Rобщ групповой средней для данного фактора.
Остаточная сумма квадратов отклонений получается как разность:
Rост = Rобщ - Rф
Для определения общей выборочной дисперсии необходимо Rобщ разделить на число измерений pq:
а для получения несмещенной общей выборочной дисперсии это выражение нужно умножить на pq/(pq-1):
Соответственно, для несмещенной факторной выборочной дисперсии:
где p-1 - число степеней свободы несмещенной факторной выборочной дисперсии.
С целью оценки влияния фактора на изменения рассматриваемого параметра рассчитывается величина:
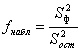
Так как отношение двух выборочных дисперсий S2ф и S2ост распределено по закону Фишера-Снедекора, то полученное значение fнабл сравнивают со значением функции распределения
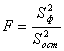
в критической точке fкр, соответствующей выбранному уровню значимости a.
Если fнабл>fкр, то фактор оказывает существенное воздействие и его следует учитывать, в противном случае он оказывает незначительное влияние, которым можно пренебречь.
Для расчета Rнабл и Rф могут быть использованы также формулы:
Rобщ=xij²-x², (4)
Rф=q∑xj²-x², (5)
Находим общую среднюю по формуле (1):
Для расчета Rобщ по формуле (4) составляем таблицу 2 квадратов вариант:
| N | П21 | П22 |
| 1 | 144 | 289 |
| 2 | 324 | 361 |
| 3 | 529 | 625 |
| 4 | 100 | 49 |
| 5 | 225 | 289 |
| ∑ | 1322 | 1613 |
Общая средняя вычисляется по формуле (1):
Rобщ = 1322 + 1613 - 5 • 2 • 16.32 = 278.1
Находим Rф по формуле (5):
Rф = 5(15.62 + 172) - 2 • 16.32 = 4.9
Получаем Rост: Rост = Rобщ - Rф = 278.1 - 4.9 = 273.2
Определяем факторную и остаточную дисперсии:
Если средние значения случайной величины, вычисленные по отдельным выборкам одинаковы, то оценки факторной и остаточной дисперсий являются несмещенными оценками генеральной дисперсии и различаются несущественно.
Тогда сопоставление оценок этих дисперсий по критерию Фишера должно показать, что нулевую гипотезу о равенстве факторной и остаточной дисперсий отвергнуть нет оснований.
Оценка факторной дисперсии меньше оценки остаточной дисперсии, поэтому можно сразу утверждать справедливость нулевой гипотезы о равенстве математических ожиданий по слоям выборки.
Иначе говоря, в данном примере фактор Ф не оказывает существенного влияния на случайную величину.
Проверим нулевую гипотезу H0: равенство средних значений х.
Находим fнабл
Для уровня значимости α=0.05, чисел степеней свободы 1 и 8 находим fкр из таблицы распределения Фишера-Снедекора.
fкр(0.05; 1; 8) = 5.32
В связи с тем, что fнабл < fкр, нулевую гипотезу о существенном влиянии фактора на результаты экспериментов отклоняем.
Другим словами, распределение вербальных и невербальных предпочтений студентов различаются.
Задание. На заводе установлено четыре линии по выпуску облицовочной плитки. С каждой линии случайным образом в течение смены отобрано по 10 плиток и сделаны замеры их толщины (мм). Отклонения от номинального размера приведены в таблице. Требуется на уровне значимости a = 0,05 установить наличие зависимости выпуска качественных плиток от линии выпуска (фактор A).
Задание. На уровне значимости a = 0,05 исследовать влияние цвета краски на срок службы покрытия.
Пример №1. Произведено 13 испытаний, из них – 4 на первом уровне фактора, 4 – на втором, 3 – на третьем и 2 на четвертом. Методом дисперсионного анализа при уровне значимости 0,05 проверить нулевую гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями. Результаты испытаний приведены в таблице.
Решение:
Находим групповые средние: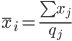
| N | П1 | П2 | П3 | П4 |
| 1 | 1.38 | 1.41 | 1.32 | 1.31 |
| 2 | 1.38 | 1.42 | 1.33 | 1.33 |
| 3 | 1.42 | 1.44 | 1.34 | - |
| 4 | 1.42 | 1.45 | - | - |
| ∑ | 5.6 | 5.72 | 3.99 | 2.64 |
| x | 1.4 | 1.43 | 1.33 | 1.32 |
В последней строке помещены групповые средние для каждого уровня фактора.
Общая средняя вычисляется по формуле:
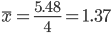
Для расчета Sобщ по формуле (4) составляем таблицу 2 квадратов вариант:
| N | П21 | П22 | П23 | П24 |
| 1 | 1.9 | 1.99 | 1.74 | 1.72 |
| 2 | 1.9 | 2.02 | 1.77 | 1.77 |
| 3 | 2.02 | 2.07 | 1.8 | - |
| 4 | 2.02 | 2.1 | - | - |
| ∑ | 7.84 | 8.18 | 5.31 | 3.49 |
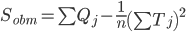
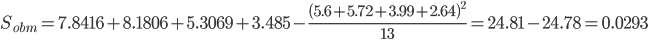
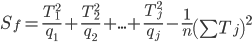
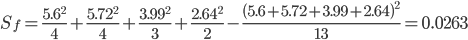
Получаем Sост: Sост = Sобщ - Sф = 0.0293 - 0.0263 = 0.003
Определяем факторную дисперсию:
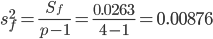
и остаточную дисперсию:
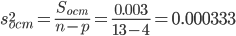
Если средние значения случайной величины, вычисленные по отдельным выборкам одинаковы, то оценки факторной и остаточной дисперсий являются несмещенными оценками генеральной дисперсии и различаются несущественно.
Тогда сопоставление оценок этих дисперсий по критерию Фишера должно показать, что нулевую гипотезу о равенстве факторной и остаточной дисперсий отвергнуть нет оснований.
Оценка факторной дисперсии больше оценки остаточной дисперсии, поэтому можно сразу утверждать не справедливость нулевой гипотезы о равенстве математических ожиданий по слоям выборки.
Иначе говоря, в данном примере фактор Ф оказывает существенное влияния на случайную величину.
Проверим нулевую гипотезу H0: равенство средних значений х.
Находим fнабл
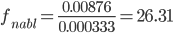
Для уровня значимости α=0.05, чисел степеней свободы 3 и 12 находим fкр из таблицы распределения Фишера-Снедекора.
fкр(0.05; 3; 12) = 3.49
В связи с тем, что fнабл > fкр, нулевую гипотезу о существенном влиянии фактора на результаты экспериментов принимаем (нулевую гипотезу о равенстве групповых средних отвергаем). Другими словами, групповые средние в целом различаются значимо.
Пример №2. В школе 5 шестых классов. Психологу ставится задача, определить, одинаковый ли средний уровень ситуативной тревожности в классах. Для этого были приведены в таблице. Проверить уровень значимости α=0.05 предположение, что средняя ситуативная тревожность в классах не различается.
Пример №3. Для изучения величины X произведено 4 испытания на каждом из пяти уровней фактора F. Результаты испытаний приведены в таблице. Выяснить, существенно ли влияние фактора F на величину X. Принять α = 0.05. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
Пример №4. Предположим, что в педагогическом эксперименте участвовали три группы студентов по 10 человек в каждой. В группах применили различные методы обучения: в первой – традиционный (F1), во второй – основанный на компьютерных технологиях (F2), в третьей – метод, широко использующий задания для самостоятельной работы (F3). Знания оценивались по десятибалльной системе.
Требуется обработать полученные данные об экзаменах и сделать заключение о том, значимо ли влияние метода преподавания, приняв за уровень значимости α=0.05.
Результаты экзаменов заданы таблицей, Fj – уровень фактора xij – оценка i-го учащегося обучающегося по методике Fj.
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Уровень фактора Fj | F1 | 7 | 5 | 6 | 4 | 6 | 7 | 8 | 6 | 5 | 7 |
| F2 | 9 | 8 | 10 | 8 | 7 | 10 | 10 | 9 | 7 | 6 | |
| F3 | 6 | 7 | 6 | 6 | 9 | 5 | 7 | 8 | 7 | 8 |
Пример №5. Показаны результаты конкурсного сортоиспытания культур (урожайность в ц.с га). Каждый сорт испытывался на четырех участках. Методом дисперсионного анализа изучите влияние сорта на урожайность. Установите существенность влияния фактора (долю межгрупповой вариации в общей вариации) и значимость результатов опыта при уровне значимости 0,05.
Урожайность на сортоиспытательных участках
| Сорт | Урожайность по повторностям ц. с га | |||
| 1 | 2 | 3 | 4 | |
| 1 2 3 | 42,4 52,5 52,3 | 37,4 50,1 53,0 | 40,7 53,8 51,4 | 38,2 50,7 53,6 |