Коэффициент контингенции
Коэффициент контингенции равен коэффициенту корреляции между X и Y и служит для измерения силы связи показателей, измеренных в номинальной шкале.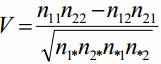
Назначение сервиса. С помощью калькулятора производится расчет коэффициента контингенции в онлайн режиме. Полученное решение сохраняется в файле Word.
2x2.
Пример. Получено выборочное распределение отношения респондентов к покупке товара «А» в зависимости от пола. Результаты приведены в таблице:
| мужчина | женщины | ni* | |
| купили | 35 | 15 | 50 |
| не купили | 10 | 30 | 40 |
| n*j | 45 | 45 | 90 |
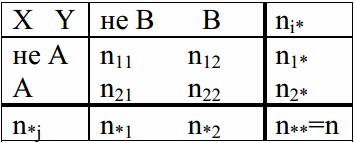
Получено выборочное распределение признака «А» в зависимости от B. Результаты приведены в таблице:
Для проверки независимости признаков «A» и «B» проверяем нулевую гипотезу Н0:(pij = pi*p*j для всех i, j). Вычислим статистику χ2 набл по формуле:
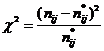
где nij – наблюдаемые частоты.
Если значение χ2набл попало в критическую область: χ2 > χ2крит(α ; v=1), нулевая гипотеза отвергается с вероятностью ошибки α и признаки считаются зависимыми.
В этом случае имеет смысл измерить полученную связь между X и Y с помощью коэффициентов связи (сопряженности).
Рассчитаем теоретические частоты по формуле:
Получим таблицу сопряженности теоретических частот распределения:
| A1 | A2 | ni* | |
| P1 | 25 | 25 | 50 |
| P2 | 20 | 20 | 40 |
| n*j | 45 | 45 | 90 |
Вычислим статистику χ2:
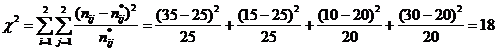
χ2крит(0.05;1) = 3.84146
где v = (r-1)(s-1) = (2-1)(2-1) = 1 - число степеней свободы.
Критическая область имеет вид χ2 > χ2крит. Так как вычисленное значение хи-квадрат попадает в критическую область, то гипотеза о независимости отвергается с вероятностью ошибки 0,05.
Воспользуемся критерием χ2*
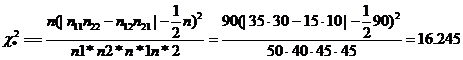
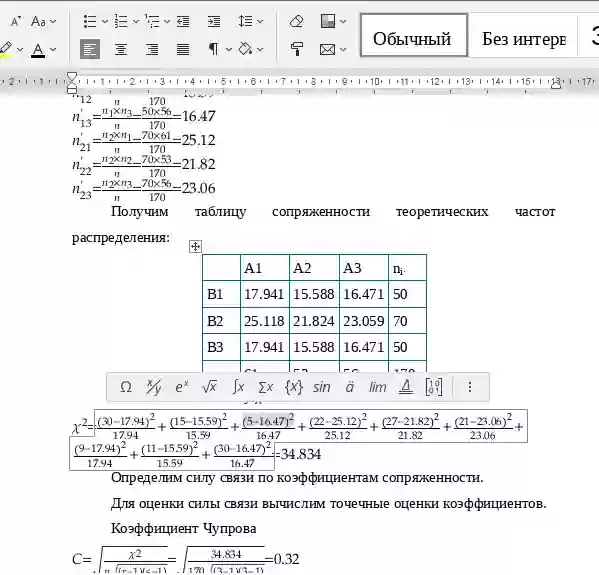
Определим силу связи по коэффициентам сопряженности.
Коэффициент ассоциации:
![]()
Коэффициент коллигации:
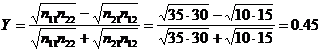
Коэффициент контингенции
![]()
Коэффициент φ (Коэффициент Чупрова-Крамера)
![]()
τ-коэффициент (коэффициент Гудмена-Краскала):
![]()
Коэффициент сопряженности Пирсона:
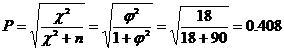
Таким образом, связь между желанием приобрести товар «А» и полом средняя.
Пример №2. Есть ли статистически значимая связь между удовлетворенностью перспективами должностного и профессионального роста в зависимости от пола респондента.
| пол | удовлетворенность | Σ | |
| доволен | не доволен | ||
| Ж | 4 | 8 | 12 |
| М | 12 | 6 | 18 |
| Σ | 16 | 14 | 30 |
Решение находим с помощью калькулятора. Для проверки независимости признаков «A» и «B» проверяем нулевую гипотезу Н0:(pij = pi*p*j для всех i, j). Вычислим статистику Χ2 набл по формуле:
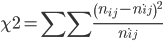
где nij – наблюдаемые частоты.
Если значение Χ2набл попало в критическую область: Χ2> Χ2крит(α ;v=1), нулевая гипотеза отвергается с вероятностью ошибки α и признаки считаются зависимыми.
В этом случае имеет смысл измерить полученную связь между X и Y с помощью коэффициентов связи (сопряженности).
Рассчитаем теоретические частоты по формуле: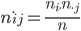
для всех клеток таблицы
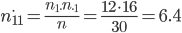
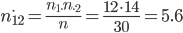
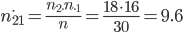
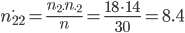
Получим таблицу сопряженности теоретических частот распределения:
| A1 | A2 | ni* | |
| P1 | 6.4 | 5.6 | 12 |
| P2 | 9.6 | 8.4 | 18 |
| n*j | 16 | 14 | 30 |
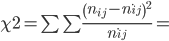
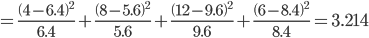
где v = (r-1)(s-1) = (2-1)(2-1) = 1 - число степеней свободы.
Критическая область имеет вид Χ2 > Χ2крит. Так как вычисленное значение хи-квадрат не попадает в критическую область, то гипотеза о независимости принимается с вероятностью ошибки 0,05.
Воспользуемся критерием Χ2*
Χ2* =
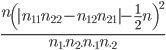 =
= 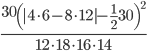 =
= 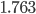
Сравнив Χ2* с Χ2крит, 1.763 < 3.84146 принимаем гипотезу о независимости.
Определим силу связи по коэффициентам сопряженности.
Коэффициент контингенции
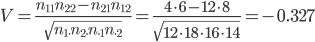
Другими словами, связь между удовлетворенностью перспективами должностного и профессионального роста в зависимости от пола респондента является хотя и зависимой, но слабой.