Пример нахождения коэффициента детерминации
Коэффициент детерминации характеризует долю вариации (дисперсии) результативного признака y, объясняемую регрессией, в общей вариации (дисперсии) y.Коэффициент детерминации рассчитывается для оценки качества подбора уравнения регрессии. Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 50%. Модели с коэффициентом детерминации выше 80% можно признать достаточно хорошими. Значение коэффициента детерминации R2 = 1 означает функциональную зависимость между переменными.
Для линейной зависимости коэффициент детерминации равен квадрату коэффициента корреляции rxy: R2 = rxy2.
Например, значение R2 = 0.83, означает, что в 83% случаев изменения х приводят к изменению y. Другими словами, точность подбора уравнения регрессии - высокая.
В общем случае, коэффициент детерминации находится по формуле: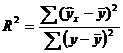 
или 
В этой формуле указаны дисперсии:
,
где ∑(y-y)2 - общая сумма квадратов отклонений;
- сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);
- остаточная сумма квадратов отклонений.
В случае нелинейной регрессии коэффициент детерминации рассчитывается через этот калькулятор. При множественной регрессии, коэффициент детемрминации можно найти через сервис Множественная регрессия
Пример. Дано:
- доля денежных доходов, направленных на прирост сбережений во вкладах, займах, сертификатах и в покупку валюты, в общей сумме среднедушевого денежного дохода, % (Y)
- среднемесячная начисленная заработная плата, тыс. руб. (X)
Уравнение имеет вид y = ax + b
1. Параметры уравнения регрессии.
Средние значения
Дисперсия.
Среднеквадратическое отклонение
Коэффициент корреляции.
Связь между признаком Y фактором X сильная и прямая.
Уравнение регрессии
Коэффициент детерминации для линейной регрессии равен квадрату коэффициента корреляции.
R 2= 0.91 2 = 0.83, т.е. в 83% случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - высокая
| x | y | x 2 | y 2 | x ∙ y | y(x) | (y-y cp) 2 | (y-y(x))2 | (x-x p) 2 |
| 15.1 | 255 | 228.01 | 65025 | 3850.5 | 505.26 | 527451.17 | 62630.22 | 420.25 |
| 17 | 261 | 289 | 68121 | 4437 | 549.38 | 518772.07 | 83161.41 | 345.96 |
| 12 | 293 | 144 | 85849 | 3516 | 433.28 | 473699.53 | 19678.51 | 556.96 |
| 10 | 310 | 100 | 96100 | 3100 | 386.84 | 450587.75 | 5904.58 | 655.36 |
| 74 | 1425 | 5476 | 2030625 | 105450 | 1872.88 | 196906.67 | 200600 | 1474.56 |
| 83 | 1985 | 6889 | 3940225 | 164755 | 2081.86 | 1007497.33 | 9381.6 | 2246.76 |
| 85 | 2549 | 7225 | 6497401 | 216665 | 2128.3 | 2457813.93 | 176990.6 | 2440.36 |
| 81 | 2012 | 6561 | 4048144 | 162972 | 2035.42 | 1062428.38 | 548.49 | 2061.16 |
| 22 | 1562 | 484 | 2439844 | 34364 | 665.47 | 337260.88 | 803758.38 | 184.96 |
| 10 | 386 | 100 | 148996 | 3860 | 386.84 | 354332.48 | 0.71 | 655.36 |
| 4 | 383 | 16 | 146689 | 1532 | 247.52 | 357913.03 | 18353.53 | 998.56 |
| 14.1 | 354.1 | 198.81 | 125386.81 | 4992.81 | 482.04 | 393327.58 | 16368.87 | 462.25 |
| 427.2 | 11775.1 | 27710.82 | 19692405.81 | 709494.31 | 11775.1 | 8137990.81 | 1397376.9 | 12502.5 |
Значимость коэффициента корреляции
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;a) = (10;0.05) = 1.812
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически - значим
Анализ точности определения оценок коэффициентов регрессии
S a = 3.3432
Доверительные интервалы для зависимой переменной
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 1
(-557.64;913.38)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика
Статистическая значимость коэффициента регрессии a подтверждается (6.95>1.812).
Статистическая значимость коэффициента регрессии b не подтверждается (0.96<1.812).
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими (tтабл=1.812):
(a - tтабл·Sa; a + tтабл·Sa)
(17.1616;29.2772)
(b - tтабл·Sb; b + tтабл·Sb)
(-136.4585;445.7528)
2) F-статистики
Fkp = 4.96
Поскольку F > Fkp, то коэффициент детерминации статистически значим