Расчет параметров уравнения тренда
Назначение сервиса. Сервис используется для расчета параметров тренда временного ряда yt онлайн с помощью метода наименьших квадратов (МНК), а также способом от условного нуля. Для этого строится система уравнений:a0n + a1∑t = ∑y
a0∑t + a1∑t2 = ∑y•t
и таблица следующего вида:
| t | y | t 2 | y 2 | t•y | y(t) |
| 1 | |||||
| ... | ... | ... | ... | ... | ... |
| N | |||||
| ИТОГО | ∑ | ∑ | ∑ | ∑ | ∑ |
Способ отсчета времени от условного начала
Для определения параметров математической функции при анализе тренда в рядах динамики используется способ отсчета времени от условного начала. Он основан на обозначении в ряду динамики показаний времени таким образом, чтобы ∑ti. При этом в ряду динамики с нечетным числом уровней порядковый номер уровня, находящегося в середине ряда, обозначают через нулевое значение и принимают его за условное начало отсчета времени с интервалом +1 всех последующих уровней и –1 всех предыдущих уровней. Например, при обозначения времени будут: –2, –1, 0, +1, +2. При четном числе уровней порядковые номера верхней половины ряда (от середины) обозначаются числами:–1, –3, –5, а нижней половины ряда обозначаются +1, +3, +5.
Пример. Статистическое изучение динамики численности населения.
- С помощью цепных, базисных, средних показателей динамики оцените изменение численности, запишите выводы.
- С помощью метода аналитического выравнивания (по прямой и параболе, определив коэффициенты с помощью МНК) выявите основную тенденцию в развитии явления (численность населения Республики Коми). Оцените качество полученных моделей с помощью ошибок и коэффициентов аппроксимации.
- Определите коэффициенты линейного и параболического трендов с помощью средств «Мастера диаграмм». Дайте точечный и интервальный прогнозы численности на 2010 г. Запишите выводы.
| 1990 | 1996 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 |
| 1249 | 1133 | 1043 | 1030 | 1016 | 1005 | 996 | 985 | 975 | 968 |
1. Находим параметры уравнения методом наименьших квадратов. Используем способ отсчета времени от условного начала.
Система уравнений МНК для линейного тренда имеет вид:
a0n + a1∑t = ∑y
a0∑t + a1∑t2 = ∑y•t
| t | y | t2 | y2 | t y |
| -9 | 1249 | 81 | 1560001 | -11241 |
| -7 | 1133 | 49 | 1283689 | -7931 |
| -5 | 1043 | 25 | 1087849 | -5215 |
| -3 | 1030 | 9 | 1060900 | -3090 |
| -1 | 1016 | 1 | 1032256 | -1016 |
| 1 | 1005 | 1 | 1010025 | 1005 |
| 3 | 996 | 9 | 992016 | 2988 |
| 5 | 985 | 25 | 970225 | 4925 |
| 7 | 975 | 49 | 950625 | 6825 |
| 9 | 968 | 81 | 937024 | 8712 |
| 0 | 10400 | 330 | 10884610 | -4038 |
10a0 + 0a1 = 10400
0a0 + 330a1 = -4038
Из первого уравнения выражаем а0 и подставим во второе уравнение
Получаем a0 = -12.236, a1 = 1040
Уравнение тренда:
y = -12.236 t + 1040
Оценим качество уравнения тренда с помощью ошибки абсолютной аппроксимации.
![]()
Ошибка аппроксимации в пределах 5%-7% свидетельствует о хорошем подборе уравнения тренда к исходным данным.
![]()
Поскольку ошибка меньше 7%, то данное уравнение можно использовать в качестве тренда.
б) выравнивание по параболе
Уравнение тренда имеет вид y = at2 + bt + c
1. Находим параметры уравнения методом наименьших квадратов.
Система уравнений МНК:
a0n + a1∑t + a2∑t2 = ∑y
a0∑t + a1∑t2 + a2∑t3 = ∑yt
a0∑t2 + a1∑t3 + a2∑t4 = ∑yt2
| t | y | t2 | y2 | t y | t3 | t4 | t2 y |
| -9 | 1249 | 81 | 1560001 | -11241 | -729 | 6561 | 101169 |
| -7 | 1133 | 49 | 1283689 | -7931 | -343 | 2401 | 55517 |
| -5 | 1043 | 25 | 1087849 | -5215 | -125 | 625 | 26075 |
| -3 | 1030 | 9 | 1060900 | -3090 | -27 | 81 | 9270 |
| -1 | 1016 | 1 | 1032256 | -1016 | -1 | 1 | 1016 |
| 1 | 1005 | 1 | 1010025 | 1005 | 1 | 1 | 1005 |
| 3 | 996 | 9 | 992016 | 2988 | 27 | 81 | 8964 |
| 5 | 985 | 25 | 970225 | 4925 | 125 | 625 | 24625 |
| 7 | 975 | 49 | 950625 | 6825 | 343 | 2401 | 47775 |
| 9 | 968 | 81 | 937024 | 8712 | 729 | 6561 | 78408 |
| 0 | 10400 | 330 | 10884610 | -4038 | 0 | 19338 | 353824 |
10a0 + 0a1 + 330a2 = 10400
0a0 + 330a1 + 0a2 = -4038
330a0 + 0a1 + 19338a2 = 353824
Получаем a0 = 1.258, a1 = -12.236, a2 = 998.5
Уравнение тренда:
y = 1.258t2-12.236t+998.5
Ошибка аппроксимации для параболического уравнения тренда.
![]()
Поскольку ошибка меньше 7%, то данное уравнение можно использовать в качестве тренда.
Минимальная ошибка аппроксимации при выравнивании по параболе. К тому же коэффициент детерминации R2 выше чем при линейной. Следовательно, для прогнозирования необходимо использовать уравнение по параболе.
Интервальный прогноз.
Определим среднеквадратическую ошибку прогнозируемого показателя.
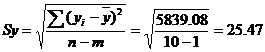
m = 1 - количество влияющих факторов в уравнении тренда.
Uy = yn+L ± K
где
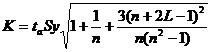
L - период упреждения; уn+L - точечный прогноз по модели на (n + L)-й момент времени; n - количество наблюдений во временном ряду; Sy - стандартная ошибка прогнозируемого показателя; Tтабл - табличное значение критерия Стьюдента для уровня значимости α и для числа степеней свободы, равного n-2.
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;α/2) = (8;0.025) = 2.306
Точечный прогноз, t = 10: y(10) = 1.26*102 -12.24*10 + 998.5 = 1001.89 тыс. чел.
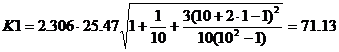
1001.89 - 71.13 = 930.76 ; 1001.89 + 71.13 = 1073.02
Интервальный прогноз:
t = 9+1 = 10: (930.76;1073.02)
Пример №2. Покажем пример подробного расчета параметров уравнения тренда на основе следующих данных (см. таблицу).
Линейное уравнение тренда имеет вид y = at + b.
1. Находим параметры уравнения методом наименьших квадратов.
Система уравнений МНК:
a0n + a1∑t = ∑y
a0∑t + a1∑t2 = ∑y•t
| t | y | t 2 | y 2 | t•y | y(t) | (y-y cp) 2 | (y-y(t))2 | (t-t p) 2 | (y-y(t)) : y |
| 1 | 17.4 | 1 | 302.76 | 17.4 | 12.26 | 895.01 | 26.47 | 30.25 | 0.3 |
| 2 | 26.9 | 4 | 723.61 | 53.8 | 18.63 | 416.84 | 68.39 | 20.25 | 0.31 |
| 3 | 23 | 9 | 529 | 69 | 25 | 591.3 | 4.02 | 12.25 | 0.0872 |
| 4 | 23.7 | 16 | 561.69 | 94.8 | 31.38 | 557.75 | 58.98 | 6.25 | 0.32 |
| 5 | 27.2 | 25 | 739.84 | 136 | 37.75 | 404.68 | 111.4 | 2.25 | 0.39 |
| 6 | 34.5 | 36 | 1190.25 | 207 | 44.13 | 164.27 | 92.72 | 0.25 | 0.28 |
| 7 | 50.7 | 49 | 2570.49 | 354.9 | 50.5 | 11.45 | 0.0383 | 0.25 | 0.0039 |
| 8 | 61.4 | 64 | 3769.96 | 491.2 | 56.88 | 198.34 | 20.44 | 2.25 | 0.0736 |
| 9 | 69.3 | 81 | 4802.49 | 623.7 | 63.25 | 483.27 | 36.56 | 6.25 | 0.0872 |
| 10 | 94.4 | 100 | 8911.36 | 944 | 69.63 | 2216.84 | 613.62 | 12.25 | 0.26 |
| 11 | 61.1 | 121 | 3733.21 | 672.1 | 76 | 189.98 | 222.11 | 20.25 | 0.24 |
| 12 | 78.2 | 144 | 6115.24 | 938.4 | 82.38 | 953.78 | 17.46 | 30.25 | 0.0534 |
| 78 | 567.8 | 650 | 33949.9 | 4602.3 | 567.8 | 7083.5 | 1272.21 | 143 | 2.41 |
12a0 + 78a1 = 567.8
78a0 + 650a1 = 4602.3
Из первого уравнения выражаем а0 и подставим во второе уравнение
Получаем a0 = 6.37, a1 = 5.88
Примечание: значения столбца №6 y(t) рассчитываются на основе полученного уравнения тренда. Например, t = 1: y(1) = 6.37*1 + 5.88 = 12.26
Уравнение тренда
y = 6.37 t + 5.88Оценим качество уравнения тренда с помощью ошибки абсолютной аппроксимации.
![]()
![]()
Поскольку ошибка больше 15%, то данное уравнение не желательно использовать в качестве тренда.
Средние значения:
![]()
![]()
![]()
Дисперсия
![]()
![]()
Среднеквадратическое отклонение
![]()
![]()
Коэффициент эластичности
![]()
![]()
Коэффициент эластичности меньше 1. Следовательно, при изменении Х на 1%, Y изменится менее чем на 1%. Другими словами - влияние Х на Y не существенно.
Коэффициент детерминации
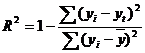
т.е. в 82.04 % случаев влияет на изменение данных. Другими словами - точность подбора уравнения тренда - высокая
2. Анализ точности определения оценок параметров уравнения тренда.
Дисперсия ошибки уравнения.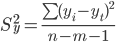
где m = 1 - количество влияющих факторов в модели тренда.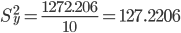
Стандартная ошибка уравнения.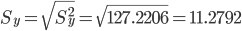
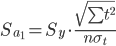
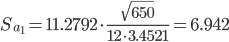
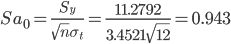
3. Проверка гипотез относительно коэффициентов линейного уравнения тренда.
1) t-статистика. Критерий Стьюдента.
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;α/2) = (10;0.025) = 2.228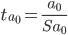
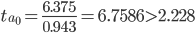
Статистическая значимость коэффициента a0 подтверждается. Оценка параметра a0 является значимой и тренд у временного ряда существует..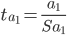
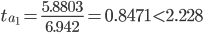
Статистическая значимость коэффициента a1 не подтверждается.
Доверительный интервал для коэффициентов уравнения тренда.
Определим доверительные интервалы коэффициентов тренда, которые с надежность 95% будут следующими:
(a1 - tнабл Sa1;a1 + tнабл Sa1)
(6.375 - 2.228*0.943; 6.375 + 2.228*0.943)
(4.27;8.48)
(a0 - tнабл Sa0;a0 + tнабл Sa0)
(5.88 - 2.228*6.942; 5.88 + 2.228*6.942)
(-9.59;21.35)
Так как точка 0 (ноль) лежит внутри доверительного интервала, то интервальная оценка коэффициента a0 статистически незначима.
2) F-статистика. Критерий Фишера.
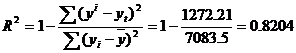
![]()
Fkp = 4.84
Поскольку F > Fkp, то коэффициент детерминации статистически значим
Проверка на наличие автокорреляции остатков
Проверка наличия гетероскедастичности
Пример №3. В таблице представлены данные, характеризующие динамику продаж некоторой продукции. Определить оптимальный тренд и оценить его значимость на уровне значимости равным 0,05. Дать точечный прогноз и с надежностью 0,95 интервальный прогноз среднего и индивидуального значений реализации продукции на одиннадцатый год.
Решение.
Скачать