Метод аналитического выравнивания
Метод аналитического выравнивания заключается в построении уравнения регрессии, характеризующего зависимость уровней ряда от временной переменной.Назначение сервиса. Сервис позволит прямо на сайте в онлайн-режиме провести аналитическое выравнивание ряда yt, проверить наличие гетероскедастичности и автокорреляции остатков тестом Дарбина-Уотсона (см. пример аналитического выравнивания по прямой).
Чтобы привести нелинейные зависимости к линейной используют метод выравнивания (линеаризацию).
| y = f(x) | Преобразование | Метод линеаризации |
| y = b xa | Y = ln(y); X = ln(x) | Логарифмирование |
| y = b eax | Y = ln(y); X = x | Комбинированный |
| y = 1/(ax+b) | Y = 1/y; X = x | Замена переменных |
| y = x/(ax+b) | Y = x/y; X = x | Замена переменных. Пример |
| y = aln(x)+b | Y = y; X = ln(x) | Комбинированный |
| y = a + bx + cx2 | x1 = x; x2 = x2 | Замена переменных |
| y = a + bx + cx2 + dx3 | x1 = x; x2 = x2; x3 = x3 | Замена переменных |
| y = a + b/x | x1 = 1/x | Замена переменных |
| y = a + sqrt(x)b | x1 = sqrt(x) | Замена переменных |
В общем случае при аналитическом выравнивании используется метод наименьших квадратов:
- Система нормальных уравнений для линейной зависимости:
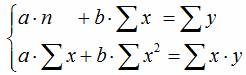
- Система нормальных уравнений для полинома второй степени (параболы):

- Система нормальных уравнений для полинома третьей степени:

Типичное задание. Произведите аналитическое выравнивание и выразите общую тенденцию развития розничного товарооборота торгового дома соответствующим аналитическим уравнением. Вычислите аналитические (выровненные) уровни ряда динамики и нанесите их на график вместе с фактическими данными.
Пример. По УР имеются данные о вводе в действие жилых домов и общежитий, тыс. м2. Для анализа динамики показателя ввода в действие жилых домов и общежитий вычислите:
- абсолютные приросты, темпы роста и темпы прироста по годам и к 1998 г., абсолютное содержание одного процента прироста. Полученные показатели представьте в виде таблицы;
- среднегодовые показатели - величину уровня ряда; абсолютный прирост темп роста и прироста. Сделайте выводы.
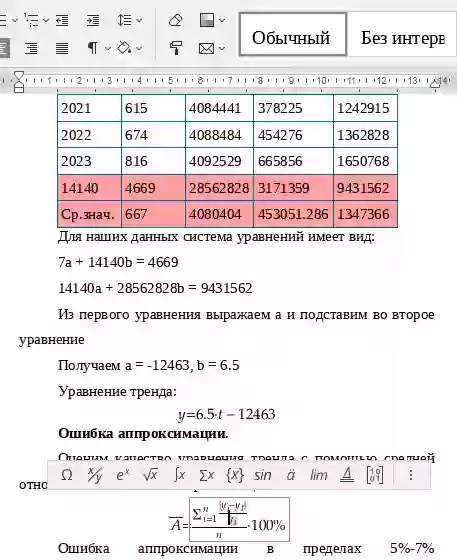
Решение. Самая простая математическая модель представляет собой линейное уравнение тренда вида y = bt + a. Чтобы найти параметры этой модели, воспользуемся методом наименьших квадратов. Система уравнений будет иметь следующий вид:
a0n + a1∑t = ∑y
a0∑t + a1∑t2 = ∑y•t
| t | y | t2 | y2 | t•y |
| 1 | 186.9 | 1 | 34931.61 | 186.9 |
| 2 | 219 | 4 | 47961 | 438 |
| 3 | 257 | 9 | 66049 | 771 |
| 4 | 276.66 | 16 | 76540.2 | 1106.64 |
| 5 | 353.5 | 25 | 124962.25 | 1767.5 |
| 6 | 310.1 | 36 | 96162.01 | 1860.6 |
| 7 | 360.9 | 49 | 130248.81 | 2526.3 |
| 8 | 371.7 | 64 | 138160.89 | 2973.6 |
| 9 | 423.9 | 81 | 179691.21 | 3815.1 |
| 45 | 2759.66 | 285 | 894706.98 | 15445.64 |
9a0 + 45a1 = 2759.66
45a0 + 285a1 = 15445.64
Данную систему уравнений можно решить несколькими методами. Получаем a0 = 27.46, a1 = 169.35. Тогда уравнение примет вид:
y = 27.46•t + 169.35