Уравнение нелинейной регрессии
Назначение сервиса. С помощью данного онлайн-калькулятора можно найти параметры уравнения нелинейной регрессии (экспоненциальной, степенной, равносторонней гиперболы, логарифмической, показательной) (см. пример).y = ax2 + bx + c), то можно воспользоваться сервисом Аналитическое выравнивание.
Ограничить однородную совокупность единиц, устранив аномальные объекты наблюдения можно через метод Ирвина или по правилу трех сигм (устранить те единицы, для которых значение объясняющего фактора отклоняется от среднего более, чем на утроенное среднеквадратичное отклонение).

Типовые задания
Исследуется зависимость производительности труда y от уровня механизации работ x (%) по данным 14 промышленных предприятий. Статистические данные приведены в таблице.
Требуется:
1) Найти оценки параметров линейной регрессии у на х. Построить диаграмму рассеяния и нанести прямую регрессии на диаграмму рассеяния.
2) На уровне значимости α=0.05 проверить гипотезу о согласии линейной регрессии с результатами наблюдений.
3) С надежностью γ=0.95 найти доверительные интервалы для параметров линейной регрессии.
Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии
Виды нелинейной регрессии
| Вид | Класс нелинейных моделей |
|
Нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам |
|
Нелинейные по оцениваемым параметрам |
Уравнению регрессии первого порядка - это уравнение парной линейной регрессии.
Уравнение регрессии второго порядка это полиномальное уравнение регрессии второго порядка: y = a + bx + cx2.

Уравнение регрессии третьего порядка соответственно полиномальное уравнение регрессии третьего порядка: y = a + bx + cx2 + dx3.

Чтобы привести нелинейные зависимости к линейной используют методы линеаризации (см. метод выравнивания):
- Замена переменных.
- Логарифмирование обеих частей уравнения.
- Комбинированный.
| y = f(x) | Преобразование | Метод линеаризации |
| y = b xa | Y = ln(y); X = ln(x) | Логарифмирование |
| y = b eax | Y = ln(y); X = x | Комбинированный |
| y = 1/(ax+b) | Y = 1/y; X = x | Замена переменных |
| y = x/(ax+b) | Y = x/y; X = x | Замена переменных. Пример |
| y = aln(x)+b | Y = y; X = ln(x) | Комбинированный |
| y = a + bx + cx2 | x1 = x; x2 = x2 | Замена переменных |
| y = a + bx + cx2 + dx3 | x1 = x; x2 = x2; x3 = x3 | Замена переменных |
| y = a + b/x | x1 = 1/x | Замена переменных |
| y = a + sqrt(x)b | x1 = sqrt(x) | Замена переменных |
- Построить поле корреляции и сформулировать гипотезу о форме связи.
- Рассчитать параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессии.
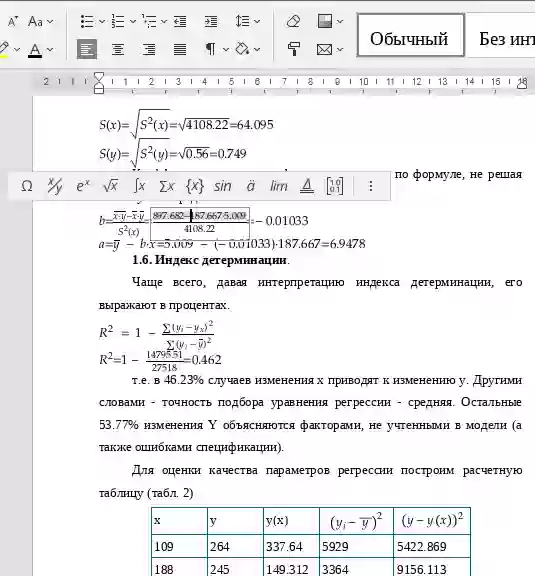
- Оценить тесноту связи с помощью показателей корреляции и детерминации.
- Дать с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
- Оценить с помощью средней ошибки аппроксимации качество уравнений.
- Оценить с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в пп. 4, 5 и данном пункте, выбрать лучшее уравнение регрессии и дать его обоснование.
- Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 15% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости
α=0,05. - Оценить полученные результаты, выводы оформить в аналитической записке.
| Год | Фактическое конечное потребление домашних хозяйств (в текущих ценах), млрд. руб. (1995 г. - трлн. руб.), y | Среднедушевые денежные доходы населения (в месяц), руб. (1995 г. - тыс. руб.), х |
| 1995 | 872 | 515,9 |
| 2000 | 3813 | 2281,1 |
| 2001 | 5014 | 3062 |
| 2002 | 6400 | 3947,2 |
| 2003 | 7708 | 5170,4 |
| 2004 | 9848 | 6410,3 |
| 2005 | 12455 | 8111,9 |
| 2006 | 15284 | 10196 |
| 2007 | 18928 | 12602,7 |
| 2008 | 23695 | 14940,6 |
| 2009 | 25151 | 16856,9 |
Решение. В калькуляторе последовательно выбираем виды нелинейной регрессии. Получим таблицу следующего вида.
Экспоненциальное уравнение регрессии имеет вид y = a ebx
После линеаризации получим: ln(y) = ln(a) + bx
Получаем эмпирические коэффициенты регрессии: b = 0.000162, a = 7.8132
Уравнение регрессии: y = e7.81321500e0.000162x = 2473.06858e0.000162x
Степенное уравнение регрессии имеет вид y = a xb
После линеаризации получим: ln(y) = ln(a) + b ln(x)
Эмпирические коэффициенты регрессии: b = 0.9626, a = 0.7714
Уравнение регрессии: y = e0.77143204x0.9626 = 2.16286x0.9626
Гиперболическое уравнение регрессии имеет вид y = b/x + a + ε
После линеаризации получим: y=bx + a
Эмпирические коэффициенты регрессии: b = 21089190.1984, a = 4585.5706
Эмпирическое уравнение регрессии: y = 21089190.1984 / x + 4585.5706
Логарифмическое уравнение регрессии имеет вид y = b ln(x) + a + ε
Эмпирические коэффициенты регрессии: b = 7142.4505, a = -49694.9535
Уравнение регрессии: y = 7142.4505 ln(x) - 49694.9535
Показательное уравнение регрессии имеет вид y = a bx + ε
После линеаризации получим: ln(y) = ln(a) + x ln(b)
Эмпирические коэффициенты регрессии: b = 0.000162, a = 7.8132
y = e7.8132*e0.000162x = 2473.06858*1.00016x
| x | y | 1/x | ln(x) | ln(y) |
| 515.9 | 872 | 0.00194 | 6.25 | 6.77 |
| 2281.1 | 3813 | 0.000438 | 7.73 | 8.25 |
| 3062 | 5014 | 0.000327 | 8.03 | 8.52 |
| 3947.2 | 6400 | 0.000253 | 8.28 | 8.76 |
| 5170.4 | 7708 | 0.000193 | 8.55 | 8.95 |
| 6410.3 | 9848 | 0.000156 | 8.77 | 9.2 |
| 8111.9 | 12455 | 0.000123 | 9 | 9.43 |
| 10196 | 15284 | 9.8E-5 | 9.23 | 9.63 |
| 12602.7 | 18928 | 7.9E-5 | 9.44 | 9.85 |
| 14940.6 | 23695 | 6.7E-5 | 9.61 | 10.07 |
| 16856.9 | 25151 | 5.9E-5 | 9.73 | 10.13 |