Парная нелинейная регрессия и корреляция
Парная нелинейная регрессия и корреляция, подбор линеаризующего преобразования (показать на конкретном примере).Задача № 1. Изучается зависимость материалоемкости продукции от размера предприятия по 10 однородным заводам (см. таблицу).
| Показатель | Материалоемкость продукции по заводам | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Потреблено материалов на единицу продукции, кг., y | 9 | 6 | 5 | 4 | 3,7 | 3,6 | 3,5 | 6 | 7 | 3,5 |
| Выпуск продукции, тыс. ед., х | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 150 | 120 | 250 |
1. Найдите параметры уравнения
2. Оцените тесноту связи с помощью индекса корреляции.
3. Охарактеризуйте эластичность изменения материалоемкости продукции.
4. Сделайте вывод о значимости уравнения регрессии.
Для оценки параметров α и β - используют МНК (метод наименьших квадратов). Метод наименьших квадратов дает наилучшие (состоятельные, эффективные и несмещенные) оценки параметров уравнения регрессии.
Но только в том случае, если выполняются определенные предпосылки относительно случайного члена (ε) и независимой переменной (x).
Формально критерий МНК можно записать так:
S = ∑(yi - y*i)2 → min
Система нормальных уравнений.
a•n + b∑x = ∑y
a∑x + b∑x2 = ∑y•x
Для наших данных система уравнений имеет вид
10a + 0.0449 b = 51.3
0.0449 a + 0.0003 b = 0.28
Из первого уравнения выражаем а и подставим во второе уравнение:
Получаем эмпирические коэффициенты регрессии: b = 592.31, a = 2.47
Уравнение регрессии (эмпирическое уравнение регрессии):
y = 592.31 / x + 2.47
Эмпирические коэффициенты регрессии a и b являются лишь оценками теоретических коэффициентов βi, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных.
Коэффициент эластичности.
Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х.
Для этих целей вычисляются коэффициенты эластичности и бета - коэффициенты.
Средний коэффициент эластичности E показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на 1% от своего среднего значения.
Коэффициент эластичности находится по формуле:
![]()
![]()
Коэффициент эластичности меньше 1. Следовательно, при изменении Х на 1%, Y изменится менее чем на 1%. Другими словами - влияние Х на Y не существенно.
Эмпирическое корреляционное отношение.
Эмпирическое корреляционное отношение вычисляется для всех форм связи и служит для измерение тесноты зависимости. Изменяется в пределах [0;1].
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < η < 0.3: слабая;
0.3 < η < 0.5: умеренная;
0.5 < η < 0.7: заметная;
0.7 < η < 0.9: высокая;
0.9 < η < 1: весьма высокая;
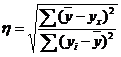
![]()
Индекс корреляции.
Величина индекса корреляции R находится в границах от 0 до 1. Чем ближе она к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии.
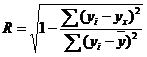
![]()
Полученная величина свидетельствует о том, что фактор x существенно влияет на y
Для любой формы зависимости теснота связи определяется с помощью множественного коэффициента корреляции:
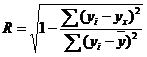
Данный коэффициент является универсальным, так как отражает тесноту связи и точность модели, а также может использоваться при любой форме связи переменных. При построении однофакторной корреляционной модели коэффициент множественной корреляции равен коэффициенту парной корреляции rxy.
В отличие от линейного коэффициента корреляции он характеризует тесноту нелинейной связи и не характеризует ее направление. Изменяется в пределах [0;1].
1.6. Индекс детерминации.
Величину R2 (равную отношению объясненной уравнением регрессии дисперсии результата у к общей дисперсии у) для нелинейных связей называют индексом детерминации.
Чаще всего, давая интерпретацию индекса детерминации, его выражают в процентах.
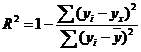
![]()
т.е. в 89.7 % случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - высокая. Остальные 10.3 % изменения Y объясняются факторами, не учтенными в модели.
| y | x 2 | y 2 | x • y | y(x) | (yi-ycp) 2 | (y-y(x))2 | (xi-xcp)2 | |y - yx|:y | |
| 0.01 | 9 | 0.0001 | 81 | 0.09 | 8.39 | 14.98 | 0.37 | 3E-05 | 0.0676 |
| 0.005 | 6 | 2.5E-05 | 36 | 0.03 | 5.43 | 0.76 | 0.32 | 0 | 0.0949 |
| 0.003333 | 5 | 1.1E-05 | 25 | 0.0167 | 4.44 | 0.0169 | 0.31 | 1E-06 | 0.11 |
| 0.0025 | 4 | 6E-06 | 16 | 0.01 | 3.95 | 1.28 | 0.002539 | 4E-06 | 0.0126 |
| 0.002 | 3.7 | 4E-06 | 13.69 | 0.0074 | 3.65 | 2.04 | 0.002166 | 6E-06 | 0.0126 |
| 0.001667 | 3.6 | 3E-06 | 12.96 | 0.006 | 3.46 | 2.34 | 0.0207 | 8E-06 | 0.04 |
| 0.001429 | 3.5 | 2E-06 | 12.25 | 0.005 | 3.31 | 2.66 | 0.0342 | 9E-06 | 0.0529 |
| 0.006667 | 6 | 4.4E-05 | 36 | 0.04 | 6.42 | 0.76 | 0.17 | 5E-06 | 0.0696 |
| 0.008333 | 7 | 6.9E-05 | 49 | 0.0583 | 7.4 | 3.5 | 0.16 | 1.5E-05 | 0.0578 |
| 0.004 | 3.5 | 1.6E-05 | 12.25 | 0.014 | 4.84 | 2.66 | 1.79 | 0 | 0.38 |
| 0.0449 | 51.3 | 0.000281 | 294.15 | 0.28 | 51.3 | 30.98 | 3.19 | 7.9E-05 | 0.9 |
Задача № 2
По данным, полученным от 20 фермерских хозяйств, выявлена зависимость объема выпуска продукции растениеводства (млн. руб.) у от четырех факторов: а) численности работников (чел.) L; б) количества минеральных удобрений на 1 га посева (кг.) М; в) количества осадков в период вегетации (мл.) R;
г) качества почвы (баллов) Q. Получены следующие варианты уравнений регрессии и доверительные интервалы коэффициентов регрессии (таблицы 1 и 2):
1) y = 2 + 0,5L + 1,7M – 2R, R2 = 0,77.
Таблица 1
| Граница | Доверительные интервалы для коэффициентов регрессии при факторе | ||
| L | M | R | |
| Нижняя | 0,1 | ??? | ??? |
| Верхняя | ??? | 2,3 | 1,5 |
2) y = 6,4 + 0,7L + 1,5L + 1,5M – 2R + 0,8Q, R2 = 0,81.
Таблица 2
| Граница | Доверительные интервалы для коэффициентов регрессии при факторе | |||
| L | M | R | Q | |
| Нижняя | 0,3 | -0,2 | ??? | 0,4 |
| Верхняя | ??? | ??? | -1,2 | 1,2 |
Задание
1. Восстановите пропущенные границы доверительных интервалов.
2. Выберите наилучшее уравнение регрессии. Дайте интерпретацию его параметров и доверительных интервалов для коэффициентов регрессии на примере одного из факторных признаков.
3. Оцените целесообразность включения в модель y фактора Q.
