Коэффициент ранговой корреляции Спирмена
Коэффициент ранговой корреляции Спирмена - это количественная оценка статистического изучения связи между явлениями, используемая в непараметрических методах.Назначение сервиса. С помощью данного онлайн-калькулятора производится:
- расчет коэффициента ранговой корреляции Спирмена;
- вычисление доверительного интервала для коэффициента и оценка его значимости;
Инструкция. Укажите количество данных (количество строк), нажмите Далее. Полученное решение сохраняется в файле Word (см пример нахождения коэффициента ранговой корреляции Спирмена). Также создается шаблон решения в Excel.
Расчет коэффициента состоит из следующих этапов:
- Ранжирование признаков по возрастанию. Ранг – это порядковый номер. Если встречаются два одинаковых значения, им присваивают одинаковое значение ранга, равное среднему арифметическому рангов этих значений.
- Определение разности рангов каждой пары сопоставляемых значений, d = dx - dy.
- Возведение в квадрат разность di и нахождение общей суммы, ∑d2.
- Вычисление коэффициента корреляции рангов по формуле:
где d2 – квадратов разностей между рангами; N – количество признаков, участвовавших в ранжировании.

Свойства коэффициента ранговой корреляции Спирмена
- Нормируемость. Коэффициент корреляции рангов может принимать значения от -1 до +1.
p = 1свидетельствует о возможном наличии прямой связи,p =-1свидетельствует о возможном наличии обратной связи. - Ограниченность. Для оценки данных необходима выборка от 5 до 40 наблюдений по каждой переменной. При большом количестве одинаковых рангов по сопоставляемым переменным коэффициент дает приближенные значения. При совпадении значений вносится поправка на одинаковые ранги. В этом случае формула имеет вид:
где d2 – квадратов разностей между рангами; Тa, Тb – поправки на одинаковые ранги; N – количество признаков, участвовавших в ранжировании.
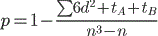
- Независимость. Чтобы получить адекватный результат, необязательно наличие нормального закона распределения коррелируемых рядов.
Область применения. Коэффициент корреляции рангов используется для оценки качества связи между двумя совокупностями. Кроме этого, его статистическая значимость применяется при анализе данных на гетероскедастичность.
Пример. По выборке данных наблюдаемых переменных X и Y:
- составить ранговую таблицу;
- найти коэффициент ранговой корреляции Спирмена и проверить его значимость на уровне 2a
- оценить характер зависимости
Решение. Присвоим ранги признаку Y и фактору X.
| X | Y | ранг X, dx | ранг Y, dy |
| 28 | 21 | 1 | 1 |
| 30 | 25 | 2 | 2 |
| 36 | 29 | 4 | 3 |
| 40 | 31 | 5 | 4 |
| 30 | 32 | 3 | 5 |
| 46 | 34 | 6 | 6 |
| 56 | 35 | 8 | 7 |
| 54 | 38 | 7 | 8 |
| 60 | 39 | 10 | 9 |
| 56 | 41 | 9 | 10 |
| 60 | 42 | 11 | 11 |
| 68 | 44 | 12 | 12 |
| 70 | 46 | 13 | 13 |
| 76 | 50 | 14 | 14 |
Матрица рангов.
| ранг X, dx | ранг Y, dy | (dx - dy)2 |
| 1 | 1 | 0 |
| 2 | 2 | 0 |
| 4 | 3 | 1 |
| 5 | 4 | 1 |
| 3 | 5 | 4 |
| 6 | 6 | 0 |
| 8 | 7 | 1 |
| 7 | 8 | 1 |
| 10 | 9 | 1 |
| 9 | 10 | 1 |
| 11 | 11 | 0 |
| 12 | 12 | 0 |
| 13 | 13 | 0 |
| 14 | 14 | 0 |
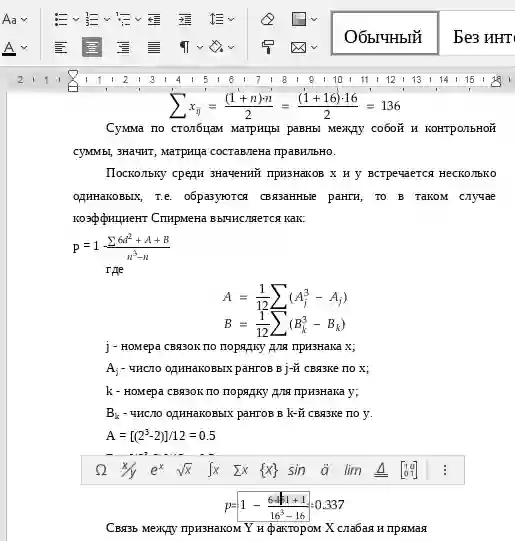
| 105 | 105 | 10 |
Проверка правильности составления матрицы на основе исчисления контрольной суммы:
Сумма по столбцам матрицы равны между собой и контрольной суммы, значит, матрица составлена правильно.
По формуле вычислим коэффициент ранговой корреляции Спирмена.
Связь между признаком Y и фактором X сильная и прямая
Значимость коэффициента ранговой корреляции Спирмена
Для того чтобы при уровне значимости α проверить нулевую гипотезу о равенстве нулю генерального коэффициента ранговой корреляции Спирмена при конкурирующей гипотезе Hi. p ≠ 0, надо вычислить критическую точку:
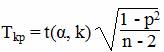
где n - объем выборки; ρ - выборочный коэффициент ранговой корреляции Спирмена: t(α, к) - критическая точка двусторонней критической области, которую находят по таблице критических точек распределения Стьюдента, по уровню значимости α и числу степеней свободы k = n-2.
Если |p| < Тkp - нет оснований отвергнуть нулевую гипотезу. Ранговая корреляционная связь между качественными признаками не значима. Если |p| > Tkp - нулевую гипотезу отвергают. Между качественными признаками существует значимая ранговая корреляционная связь.
По таблице Стьюдента находим t(α/2, k) = (0.1/2;12) = 1.782
Поскольку Tkp < ρ, то отклоняем гипотезу о равенстве 0 коэффициента ранговой корреляции Спирмена. Другими словами, коэффициент ранговой корреляции статистически - значим и ранговая корреляционная связь между оценками по двум тестам значимая.