Определитель матрицы ▦ Производная функции dydx График 3D Упростить выражение Графический метод решения задач нелинейного программирования ⇲ …
Примеры решений Коэффициент Спирмена Коэффициент Фехнера Множественная регрессия Нелинейная регрессия Уравнение регрессии Автокорреляция Расчет параметров тренда Ошибка аппроксимации

Пример нахождения коэффициента корреляции

Коэффициент корреляции
где x·y, x, y - средние значения выборок; σ(x), σ(y) - среднеквадратические отклонения.
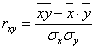
Кроме того, коэффициент линейной парной корреляции Пирсона может быть определен через коэффициент регрессии b: 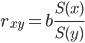коэффициент линейной парной корреляции может быть определен через коэффициент регрессии, где σ(x)=S(x), σ(y)=S(y) - среднеквадратические отклонения, b - коэффициент перед x в уравнении регрессии y=a+bx.

Другие варианты формул:
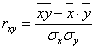или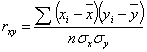

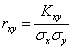
Кxy - корреляционный момент (коэффициент ковариации)
корреляционный момент
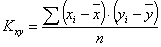
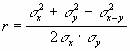Для нахождения линейного коэффициента корреляции Пирсона необходимо найти выборочные средние x и y, и их среднеквадратические отклонения σx = S(x), σy = S(y):

Линейный коэффициент корреляции указывает на наличие связи и принимает значения от –1 до +1 (см. шкалу Чеддока). Например, при анализе тесноты линейной корреляционной связи между двумя переменными получен коэффициент парной линейной корреляции, равный –1. Это означает, что между переменными существует точная обратная линейная зависимость.
Вычислить значение коэффициента корреляции можно по заданным средним выборки, либо непосредственно по исходным табличным данным.
Линейный коэффициент корреляции Пирсона
Геометрический смысл коэффициента корреляции: rxy показывает, насколько различается наклон двух линий регрессии: y(x) и х(у), насколько сильно различаются результаты минимизации отклонений по x и по y. Чем больше угол между линиями, то тем больше rxy.
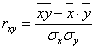
Знак коэффициента корреляции совпадает со знаком коэффициента регрессии и определяет наклон линии регрессии, т.е. общую направленность зависимости (возрастание или убывание). Абсолютная величина коэффициента корреляции определяется степенью близости точек к линии регрессии.

Свойства коэффициента корреляции

  1. |rxy| ≤ 1;, -1≤x≤1
  2. если X и Y независимы, то rxy=0, обратное не всегда верно;
  3. если |rxy|=1, то Y=aX+b, |rxy(X,aX+b)|=1, где a и b постоянные, а ≠ 0;
  4. |rxy(X,Y)|=|rxy(a1X+b1, a2X+b2)|, где a1, a2, b1, b2 – постоянные.

Поэтому для проверки направления связи выбирается проверка гипотезы при помощи коэффициента корреляции Пирсона с дальнейшей проверкой на достоверность при помощи t-критерия (пример см. ниже).

Количество строк (исходных данных)
Заданы итоговые значения величин (∑x, ∑x2, ∑xy, ∑y, ∑y2)
Здесь будет отображаться решение.
Назначение сервиса. С помощью данного онлайн-калькулятора можно найти параметры уравнения нелинейной регрессии (экспоненциальной, степенной, равносторонней гиперболы, логарифмической, показательной) (см. пример).

Инструкция. Укажите количество исходных данных. Полученное решение сохраняется в файле Word. Также автоматически создается шаблон решения в Excel.

Примечание: если необходимо определить параметры параболической зависимости (y = ax2 + bx + c), то можно воспользоваться сервисом Аналитическое выравнивание.
Ограничить однородную совокупность единиц, устранив аномальные объекты наблюдения можно через метод Ирвина или по правилу трех сигм (устранить те единицы, для которых значение объясняющего фактора отклоняется от среднего более, чем на утроенное среднеквадратичное отклонение).

Пример. На основе данных, приведенных в Приложении 1 и соответствующих Вашему варианту (таблица 2), требуется:

  1. Рассчитать коэффициент линейной парной корреляции и построить уравнение линейной парной регрессии одного признака от другого. Один из признаков, соответствующих Вашему варианту, будет играть роль факторного (х), другой – результативного (y). Причинно-следственные связи между признаками установить самим на основе экономического анализа. Пояснить смысл параметров уравнения.
  2. Определить теоретический коэффициент детерминации и остаточную (необъясненную уравнением регрессии) дисперсию. Сделать вывод.
  3. Оценить статистическую значимость уравнения регрессии в целом на пятипроцентном уровне с помощью F-критерия Фишера. Сделать вывод.
  4. Выполнить прогноз ожидаемого значения признака-результата y при прогнозном значении признака-фактора х, составляющим 105% от среднего уровня х. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал с вероятностью 0,95.
Решение. Уравнение имеет вид y = ax + b
Средние значения



Дисперсия

Среднеквадратическое отклонение


Коэффициент корреляции
Связь между признаком Y фактором X  сильная и прямая (определяется по шкале Чеддока).
Уравнение регрессии
Коэффициент регрессии: k = a = 4.01
Коэффициент детерминации
R 2 = 0.99 2 = 0.97, т.е. в 97% случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - высокая. Остаточная дисперсия: 3%.
xyx2y2x·yy(x)(yi-y)2(y-y(x))2(x-xp)2
1 107 1 11449 107 103.19 333.06 14.5 30.25
2 109 4 11881 218 107.2 264.06 3.23 20.25
3 110 9 12100 330 111.21 232.56 1.47 12.25
4 113 16 12769 452 115.22 150.06 4.95 6.25
5 120 25 14400 600 119.23 27.56 0.59 2.25
6 122 36 14884 732 123.24 10.56 1.55 0.25
7 123 49 15129 861 127.26 5.06 18.11 0.25
8 128 64 16384 1024 131.27 7.56 10.67 2.25
9 136 81 18496 1224 135.28 115.56 0.52 6.25
10 140 100 19600 1400 139.29 217.56 0.51 12.25
11 145 121 21025 1595 143.3 390.06 2.9 20.25
12 150 144 22500 1800 147.31 612.56 7.25 30.25
7815036501906171034315032366.2566.23143

Примечание: значения y(x) находятся из полученного уравнения регрессии:
y(1) = 4.01*1 + 99.18 = 103.19
y(2) = 4.01*2 + 99.18 = 107.2
... ... ...

Значимость коэффициента корреляции

Выдвигаем гипотезы:
H0: rxy = 0, нет линейной взаимосвязи между переменными;
H1: rxy ≠ 0, есть линейная взаимосвязь между переменными;
Для того чтобы при уровне значимости α проверить нулевую гипотезу о равенстве нулю генерального коэффициента корреляции нормальной двумерной случайной величины при конкурирующей гипотезе H1 ≠ 0, надо вычислить наблюдаемое значение критерия (величина случайной ошибки):
По таблице Стьюдента находим tтабл (n-m-1;α/2) = (10;0.025) = 2.228
Поскольку Tнабл > tтабл, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим.
Интервальная оценка для коэффициента корреляции (доверительный интервал)
Интервальная оценка для коэффициента корреляции

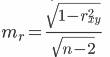
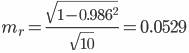
r - Δr ≤ r ≤ r + Δr
Δr = ±tтаблmr = ±2.228 • 0.0529 = 0.118
0.986 - 0.118 ≤ r ≤ 0.986 + 0.118
Доверительный интервал для коэффициента корреляции: 0.868 ≤ r ≤ 1

Анализ точности определения оценок коэффициентов регрессии





Sa=0.2152

Доверительные интервалы для зависимой переменной

Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 7
(122.4;132.11)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии

1) t-статистика


Статистическая значимость коэффициента регрессии подтверждается (18.63>2.228).

Статистическая значимость коэффициента регрессии подтверждается (62.62>2.228).
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95%  будут следующими (tтабл=2.228):
(a - tтабл·Sa; a + tтабл·S a)
(3.6205;4.4005)
(b - tтабл·Sb; b + tтабл·Sb)
(96.3117;102.0519)

2) F-статистики


Fkp = 4.96. Поскольку F > Fkp, то коэффициент детерминации статистически значим (см. критерий Фишера).

см. также Корреляционный анализ. Примеры решения задач.

Пример №2
1. Расчет средних значений x, y: x = ∑xi n = 660.6 11 = 60.05 y = ∑yi n = 333.94 11 = 30.36 x·y = ∑xi·yi n = 19952.07 11 = 1813.82
2. Расчет дисперсий: S2(x) = xi2 n - x2 = 40337.2 11 - 60.052 = 60.47 S2(y) = yi2 n - y2 = 10329.52 11 - 30.362 = 17.43 3. Расчет среднеквадратических отклонений: S(x) = √ S2(x) = √ 60.47 = 7.78 S(y) = √ S2(y) = √ 17.43 = 4.17
4. Расчет линейного коэффициента корреляции Пирсона: rxy = x·y - x·y S(x)·S(y) = 1813.82-60.05·30.36 7.78·4.17 = -0.2872 Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < rxy < 0.3: слабая;
0.3 < rxy < 0.5: умеренная;
0.5 < rxy < 0.7: заметная;
0.7 < rxy < 0.9: высокая;
0.9 < rxy < 1: весьма высокая;
В нашем примере связь между признаком Y фактором X слабая и обратная.

x yx2y2x·yy(x)(yi-y)2(y-y(x))2
68.5 22.39 4692.25 501.31 1533.72 29.06 63.49 44.44
75.7 29.24 5730.49 854.98 2213.47 27.95 1.25 1.67
52.7 32.92 2777.29 1083.73 1734.88 31.49 6.56 2.04
60.2 33.52 3624.04 1123.59 2017.9 30.34 10 10.14
62.3 30.98 3881.29 959.76 1930.05 30.01 0.39 0.94
48.3 37.17 2332.89 1381.61 1795.31 32.17 46.4 25
56.5 32.12 3192.25 1031.69 1814.78 30.91 3.1 1.47
65.9 31.76 4342.81 1008.7 2092.98 29.46 1.97 5.3
56.2 28.48 3158.44 811.11 1600.58 30.95 3.53 6.11
51.1 23.17 2611.21 536.85 1183.99 31.74 51.67 73.42
63.2 32.19 3994.24 1036.2 2034.41 29.87 3.36 5.37
660.6333.9440337.210329.5219952.07333.94191.71175.9

Значимость линейного коэффициента корреляции Пирсона. tнабл = rxy· √ n-2 √ 1-rxy2 = 0.2872· √ 9 √ 1-0.28722 = 0.9
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=n-m-1=11-1-1=9 находим tкрит: tкрит(n-m-1;α/2) = tкрит(9;0.025) = 2.262, где m=1 - количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции Пирсона признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл < tкрит, то принимаем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - не значим
В парной линейной регрессии t2r = t2b и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.

Интервальная оценка для линейного коэффициента корреляции Пирсона ( rxy - tкрит· 1-rxy2 √ n ; rxy + tкрит· 1-rxy2 √ n )
Доверительный интервал для коэффициента корреляции ( 0.29 - 2.262· 1-0.292 √ 11 ; 0.29 + 2.262· 1-0.292 √ 11 ) Доверительный интервал для линейного коэффициента корреляции Пирсона: r(-0.9129;0.3386)

Перейти к онлайн решению своей задачи