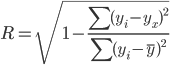Среднее квадратическое отклонение
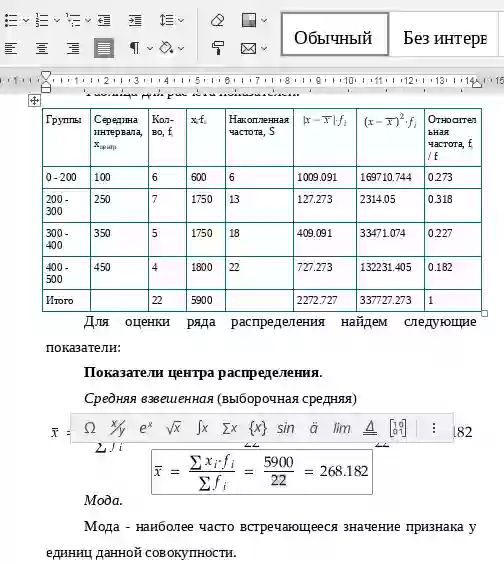
Среднеквадратическое отклонение равно квадратному корню из дисперсии: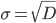
При определении среднего квадратического отклонения при достаточно большом объеме изучаемой совокупности (n > 30) применяются формулы:
– среднее квадратическое отклонение простое (или невзвешенное);
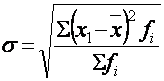– среднее квадратическое отклонение взвешенное, где:
xi – значения изучаемого признака (варианты);
n – объем статистической совокупности;
x – средняя арифметическая величина.
Среднее квадратическое отклонение характеризует разброс значений относительно среднего (математического ожидания). Обозначается как σ(x) или s(x).
Свойства среднего квадратическоо отклонения
- σ(const)=0
- σ(x)≥0
- σ(k*x)=k*σ(x)
- Среднее квадратическое отклонение суммы или разности двух независимых случайных величин равна квадратному корню от суммы квадратов квадратических отклонений этих величин.
Среднее квадратическое отклонение в рядах распределения
- Равномерное распределение
Дисперсия: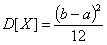
Среднеквадратическое отклонение: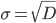
- Нормальное распределение
Дисперсия:D[X] = σ2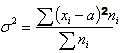
Среднеквадратическое отклонение: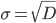
- Показательное распределение
Дисперсия:D[X] = 1/λ2
Среднеквадратическое отклонение: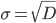
- Распределение Пуассона
Дисперсия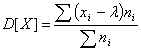
Среднеквадратическое отклонение: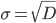
- Биномиальное распределение
ДисперсияD[X]=∑x2ipi - M[x]2
Среднеквадратическое отклонение: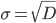
Среднее квадратическое отклонение случайных величин
- Дискретной случайной величины
Дисперсияd=∑x2ipi - M[x]2
Среднее квадратическое отклонение σ(x) = sqrt(D[X]) - Непрерывной случайной величины
Дисперсия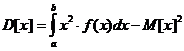
Среднее квадратическое отклонение σ(x) = sqrt(D[X]) - Системы случайных величин
Выборочные средние:
x = (20(2 + 4) + 30(6 + 3) + 40(6 + 45 + 4) + 50(2 + 8 + 6) + 60(4 + 7 + 3))/100 = 42.3
y = (20(2 + 4) + 30(6 + 3) + 40(6 + 45 + 4) + 50(2 + 8 + 6) + 60(4 + 7 + 3))/100 = 25.3
Дисперсии:
σ2x = (202(2 + 4) + 302(6 + 3) + 402(6 + 45 + 4) + 502(2 + 8 + 6) + 602(4 + 7 + 3))/100 - 42.32 = 99.71
σ2y = (112(2) + 162(4 + 6) + 212(3 + 6 + 2) + 262(45 + 8 + 4) + 312(4 + 6 + 7) + 362(3))/100 - 25.32 = 24.01
Среднеквадратические отклонения: σx = 9.99 и σy = 4.9
Дан интервальный вариационный ряд i-номер интервала, n1 – частота попадания вариант в интервал (xi; xi+1).
- построить гистограмму частот;
- вычислить несмещенную оценку дисперсии и СКО;
- вычислить среднее абсолютное отклонение θ;
- вычислить коэффициент вариации V;
- определить размах варьирования R.
