Структурные характеристики вариационного ряда распределения
Наряду со средними величинами в качестве статистических характеристик вариационных рядов распределения рассчитываются структурные средние – мода и медиана.Мода (Mo) представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой, т.е. мода – значение признака, встречающееся чаще всего.
Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности, т.е. медиана – центральное значение вариационного ряда.
Главное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины ∑|xi - Me|=min.
Определение моды и медианы по несгруппированным данным
Рассмотрим определение моды и медианы по несгруппированным данным. Предположим, рабочие бригады, состоящей из 9 человек, имеют следующие тарифные разряды:4 3 4 5 3 3 6 2 6. Так как в данной бригаде больше всего рабочих 3-го разряда, этот тарифный разряд будет модальным. Mo = 3.
Для определения медианы необходимо провести ранжирование:
2 3 3 3 4 4 5 6 6. Центральным в этом ряду является рабочий 4-го разряда, следовательно, данный разряд и будет медианным. Если ранжированный ряд включает четное число единиц, то медиана определяется как средняя из двух центральных значений.
Если мода отражает наиболее распространенный вариант значения признака, то медиана практически выполняет функции средней для неоднородной, не подчиняющейся нормальному закону распределения совокупности. Проиллюстрируем ее познавательное значение следующим примером.
Допустим, нам необходимо дать характеристику среднего дохода группы людей, насчитывающей 100 человек, из которых 99 имеют доходы в интервале от 100 до 200 долларов в месяц, а месячные доходы последнего составляют 50000 долларов (табл. 1).
Таблица 1 - Месячные доходы исследуемой группы людей.
| N п/п | 1 | 2 | 3 | 4 | … | 50 | 51 | … | 99 | 100 |
| Доход, долл. | 100 | 104 | 104 | 107 | … | 162 | 164 | … | 100 | 50 000 |
Рассмотрим определение моды и медианы по сгруппированным данным (рядам распределения).
Предположим, распределение рабочих всего предприятия в целом по тарифному разряду имеет следующий вид (табл. 2).
Таблица 2 - Распределение рабочих предприятия по тарифному разряду
| Тарифный разряд | Численность рабочих, человек |
| 2 | 12 |
| 3 | 48 |
| 4 | 56 |
| 5 | 60 |
| 6 | 14 |
| ВСЕГО | 190 |
Моду и медиану можно найти с помощью онлайн-калькуляторов.
Расчет моды и медианы для дискретного ряда
Расчет моды и медианы для интервального ряд
Расчет моды и медианы для вариационного ряда
Определение моды по дискретному вариационному ряду
Используется построенный ранее ряд значений признака, отсортированных по величине. Если объем выборки нечетный, берем центральное значение; если объем выборки четный, берем среднее арифметическое двух центральных значений.Определение моды по дискретному вариационному ряду: наибольшую частоту (60 человек) имеет 5-й тарифный разряд, следовательно, он и является модальным. Mo = 5.
Для определения медианного значения признака по следующей формуле находят номер медианной единицы ряда (NMe):
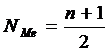, где n - объем совокупности.
В нашем случае:
.
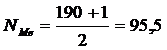Полученное дробное значение, всегда имеющее место при четном числе единиц совокупности, указывает, что точная середина находится между 95 и 96 рабочими. Необходимо определить, к какой группе относятся рабочие с этими порядковыми номерами. Это можно сделать, рассчитав накопленные частоты. Рабочих с этими номерами нет в первой группе, где всего лишь 12 человек, нет их и во второй группе (12+48=60). 95-й и 96-й рабочие находятся в третьей группе (12+48+56=116), следовательно, медианным является 4-й тарифный разряд.
Моду и медиану можно найти с помощью онлайн-калькуляторов.
Расчет моды и медианы в интервальном ряду
В отличие от дискретных вариационных рядов определение моды и медианы по интервальным рядам требует проведения определенных расчетов на основе следующих формул: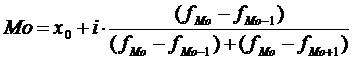
, (6)i – величина модального интервала;
fMo – частота модального интервала;
fMo-1 – частота интервала, предшествующего модальному;
fMo+1 – частота интервала, следующего за модальным.
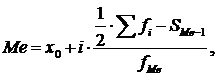(7)
где x0 – нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот);
i – величина медианного интервала;
SMe-1 – накопленная интервала, предшествующего медианному;
fMe – частота медианного интервала.
Проиллюстрируем применение этих формул, используя данные табл. 3.
Интервал с границами 60 – 80 в данном распределении будет модальным, т.к. он имеет наибольшую частоту. Использую формулу (6), определим моду:
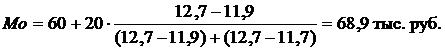
Установили, что медианным является интервал с границами 100 – 120 тыс. руб. Определим теперь медиану:
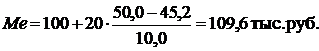
Таблица 3 - Распределение населения РФ по уровню среднедушевых номинальных денежных доходов в марте 1994г.
| Группы по уровню среднедушевого месячного дохода, тыс. руб. | Удельный вес населения, % |
| До 20 | 1,4 |
| 20 – 40 | 7,5 |
| 40 – 60 | 11,9 |
| 60 – 80 | 12,7 |
| 80 – 100 | 11,7 |
| 100 – 120 | 10,0 |
| 120 – 140 | 8,3 |
| 140 –160 | 6,8 |
| 160 – 180 | 5,5 |
| 180 – 200 | 4,4 |
| 200 – 220 | 3,5 |
| 220 – 240 | 2,9 |
| 240 – 260 | 2,3 |
| 260 – 280 | 1,9 |
| 280 – 300 | 1,5 |
| Свыше 300 | 7,7 |
| Итого | 100,0 |
Таблица 4 - Определение медианного интервала
| Интервал, тыс. руб. | Накопленная частота, % |
| До 20 | 1,4 |
| 20 – 40 | 8,9 |
| 40 – 60 | 20,8 |
| 60 – 80 | 33,5 |
| 80 – 100 | 45,2 |
| 100 – 120 | 55,2 |
Таким образом, в качестве обобщенной характеристики значений определенного признака у единиц ранжированной совокупности могут быть использованы средняя арифметическая, мода и медиана.
Основной характеристикой центра распределения является средняя арифметическая, для которой характерно то, что все отклонения от нее (положительные и отрицательные) в сумме равняются нулю. Для медианы характерно, что сумма отклонений от нее по модулю является минимальной, а мода представляет собой значение признака, которое наиболее часто встречается.
Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию. В симметричных распределениях все три характеристики совпадают. Чем больше расхождение между модой и средней арифметической, тем более асимметричен ряд. Для умеренно асимметричных рядов разность между модой и средней арифметической примерно в три раза превышает разность между медианой и средней, т.е.:
|Mo –`x| = 3 |Me –`x|.
Определение моды и медианы графическим методом
Моду и медиану в интервальном ряду можно определить графически. Мода определяется по гистограмме распределения. Для этого выбирается самый высокий прямоугольник, который является в данном случае модальным. Затем правую вершину модального прямоугольника соединяем с правым верхним углом предыдущего прямоугольника. А левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Из точки их пересечения опускаем перпендикуляр на ось абсцисс. Абсцисса точки пересечения этих прямых и будет модой распределения (рис. 3).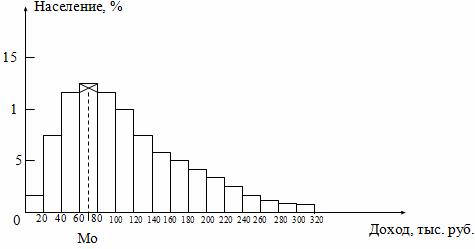
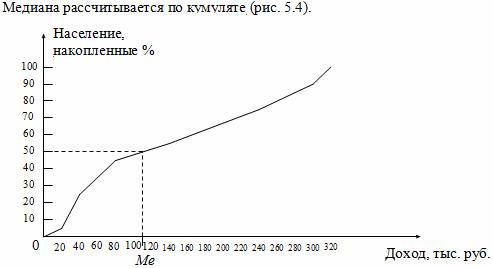
Для определения медианы из точки на шкале накопленных частот (частостей), соответствующей 50 %, проводится прямая, параллельная оси абсцисс до пересечения с кумулятой. Затем из точки пересечения опускается перпендикуляр на ось абсцисс. Абсцисса точки пересечения является медианой.
Квартили, децили, перцентили
Аналогично с нахождением медианы в вариационных рядах распределения можно отыскать значение признака у любой по порядку единицы ранжированного ряда. Так, например, можно найти значение признака у единиц, делящих ряд на четыре равные части, на 10 или на 100 частей. Эти величины называются «квартили», «децили», «перцентили».Квартили представляют собой значение признака, делящее ранжированную совокупность на 4 равновеликие части.
Различают квартиль нижний (Q1), отделяющий ¼ часть совокупности с наименьшими значениями признака, и квартиль верхний (Q3), осекающий ¼ часть с наибольшими значениями признака. Это означает, что 25 % единиц совокупности будут меньше по величине Q1; 25 % единиц будут заключены между Q1 и Q2; 25 % - между Q2 и Q3, а остальные 25 % превосходят Q3. Средним квартилем Q2 является медиана.
Для расчета квартилей по интервальному вариационному ряду используются формулы:
, 
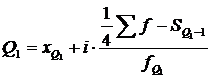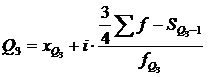
где xQ1 – нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25 %);
xQ3 – нижняя граница интервала, содержащего верхний квартиль (интервал определяется по накопленной частоте, первой превышающей 75 %);
i – величина интервала;
SQ1-1 – накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль;
SQ3-1 – накопленная частота интервала, предшествующего интервалу, содержащему верхний квартиль;
fQ1 – частота интервала, содержащего нижний квартиль;
fQ3 – частота интервала, содержащего верхний квартиль.
Рассмотрим расчет нижнего и верхнего квартилей по данным табл. 10. Нижний квартиль находится в интервале 60 – 80, накопленная частота которого равна 33,5 %. Верхний квартиль лежит в интервале 160 – 180 с накопленной частотой 75,8 %. С учетом этого получим:
,
.
Вычисляются они по формулам:
, 
.
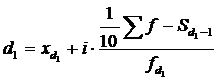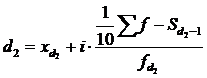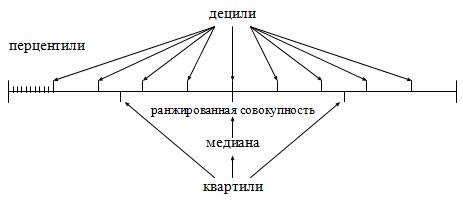
Значения признака, делящие ряд на сто частей, называются перцентилями. Соотношения медианы, квартилей, децилей и перцентилей представлены на рис. 5.
Квартили и децили можно найти с помощью онлайн-калькуляторов.