Критерий Манна-Уитни
Назначение сервиса. С помощью данного онлайн-калькулятора производится расчет U критерия Манна-Уитни.
Инструкция. Укажите количество данных (количество строк). Полученное решение сохраняется в файле Word.
Назначение критерия
Критерий предназначен для оценки различий между двумя выборками по уровню какого-либо признака, количественно измеренного. Он позволяет выявлять различия между малыми выборками, когда n1, n2 ≥ 3 или n1=2, n2 ≥ 5. В каждой выборке должно быть не более 60 наблюдений.Этот метод определяет, достаточно ли мала зона перекрещивающихся значений между двумя рядами. Положим, что первым рядом (выборкой, группой) мы называем тот ряд значений, в котором значения, по предварительной оценке, выше, а вторым рядом - тот, где они предположительно ниже.
Чем меньше область перекрещивающихся значений, тем более вероятно, что различия достоверны. Иногда эти различия называют различиями в расположении двух выборок.
Эмпирическое значение критерия U отражает то, насколько велика зона совпадения между рядами. Поэтому чем меньше Uэмп, тем более вероятно, что различия достоверны.
Гипотезы
H0: Уровень признака в группе 2 не ниже уровня признака в группе 1.
H1: Уровень признака в группе 2 ниже уровня признака в группе 1.
Алгоритм расчета критерия Манна-Уитни
- Объединить все данные в единый ряд, пометив данные, принадлежащие разным выборкам.
- Проранжировать значения, приписывая меньшему значению меньший ранг. Всего рангов получится (n1 + n2).
- Подсчитать сумму рангов отдельно для каждой выборки.
- Определить большую из двух ранговых сумм.
- Определить значение U по формуле:
U = n1·n2 + nx·(nx + 1)/2 – Tx,
где n1 – объем выборки №1; n2 – объем выборки №2; Tx – большая из двух ранговых сумм; nx – объем максимальной выборки: nx= max(n1, n2). - Определить критические значения Uкр по таблице. Если Uэмп > Uкр(0,05). H0 принимается. Если Uэмп ≤ Uкр(0,05) H0 отвергается. Чем меньше значения U, тем достоверность различий выше.
Пример. У предполагаемых участников психологического эксперимента был измерен уровень вербального и невербального интеллекта с помощью методики Д. Векслера. Было обследовано две группы юношей в возрасте от 18 до 24 лет студентов физического факультета и психологического факультета. Показатели вербального интеллекта представлены в таблице. Можно ли утверждать, что одна из групп превосходит другую по уровню вербального интеллекта?
| Ф | П |
| 135 | 130 |
| 130 | 129 |
| 131 | 121 |
| 128 | 129 |
| 127 | 119 |
| 137 | 124 |
| 126 | 125 |
| 137 | 129 |
| 131 | 129 |
| 137 | 130 |
| 137 | 131 |
| 127 | 123 |
| 133 | |
| 125 |
Сравнение результатов показывает, что значения выборки X несколько выше, чем выборки Y, поэтому первой считаем выборку X.
Таким образом, нам требуется определить, можно ли считать имеющуюся разницу между баллами существенной.
Решение.
Проранжируем представленную таблицу. При ранжировании объединяем две выборки в одну. Ранги присваиваются в порядке возрастания значения измеряемой величины, т.е. наименьшему рангу соответствует наименьший балл. Заметим, что в случае совпадения баллов для нескольких учеников ранг такого балла следует считать, как среднее арифметическое тех позиций, которые занимают данные баллы при их расположении в порядке возрастания.
Так как в матрице имеются связанные ранги (одинаковый ранговый номер) 1-го ряда, произведем их переформирование. Переформирование рангов производиться без изменения важности ранга, то есть между ранговыми номерами должны сохраниться соответствующие соотношения (больше, меньше или равно). Также не рекомендуется ставить ранг выше 1 и ниже значения равного количеству параметров (в данном случае n = 26). Переформирование рангов производится в табл.
| Номера мест в упорядоченном ряду | Расположение факторов по оценке эксперта | Новые ранги |
| 1 | 119 | 1 |
| 2 | 121 | 2 |
| 3 | 123 | 3 |
| 4 | 124 | 4 |
| 5 | 125 | 5.5 |
| 6 | 125 | 5.5 |
| 7 | 126 | 7 |
| 8 | 127 | 8.5 |
| 9 | 127 | 8.5 |
| 10 | 128 | 10 |
| 11 | 129 | 12.5 |
| 12 | 129 | 12.5 |
| 13 | 129 | 12.5 |
| 14 | 129 | 12.5 |
| 15 | 130 | 16 |
| 16 | 130 | 16 |
| 17 | 130 | 16 |
| 18 | 131 | 19 |
| 19 | 131 | 19 |
| 20 | 131 | 19 |
| 21 | 133 | 21 |
| 22 | 135 | 22 |
| 23 | 137 | 24.5 |
| 24 | 137 | 24.5 |
| 25 | 137 | 24.5 |
| 26 | 137 | 24.5 |
Используя предложенный принцип ранжирования, получим таблицу рангов.
| X | Ранг X | Y | Ранг Y |
| 125 | 5.5 | 119 | 1 |
| 126 | 7 | 121 | 2 |
| 127 | 8.5 | 123 | 3 |
| 127 | 8.5 | 124 | 4 |
| 128 | 10 | 125 | 5.5 |
| 130 | 16 | 129 | 12.5 |
| 131 | 19 | 129 | 12.5 |
| 131 | 19 | 129 | 12.5 |
| 133 | 21 | 129 | 12.5 |
| 135 | 22 | 130 | 16 |
| 137 | 24.5 | 130 | 16 |
| 137 | 24.5 | 131 | 19 |
| 137 | 24.5 | ||
| 137 | 24.5 | ||
| Сумма | 234.5 | Сумма | 116.5 |
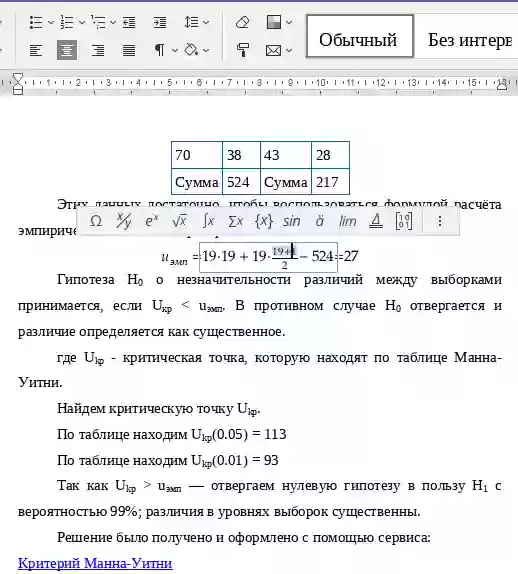
Этих данных достаточно, чтобы воспользоваться формулой расчёта эмпирического значения критерия:
Гипотеза H0 о незначительности различий между выборками принимается, если Uкр < uэмп. В противном случае H0 отвергается и различие определяется как существенное.
где Ukp - критическая точка, которую находят по таблице Манна-Уитни.
Найдем критическую точку Ukp
По таблице находим Ukp(0.05) = 45
Так как Ukp > uэмп — принимаем альтернативную гипотезу H1; различия в уровнях выборок можно считать существенными.