Пример. Значимость коэффициента корреляции
Линейное уравнение регрессии имеет видy=ax+b
1. Параметры уравнения регрессии.
Средние значения
Дисперсия
Среднеквадратическое отклонение
Коэффициент корреляции
Связь между признаком Y фактором X сильная и прямая.
Уравнение регрессии
Коэффициент детерминации
R 2= 0.9707 2 = 0.9423, т.е. в 94.24 % случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - высокая.
| x | y | x2 | y2 | x·y | y(x) | (y-y)2 | (y-y(x))2 | (x-xp)2 |
| 1 | 0.4 | 1 | 0.16 | 0.4 | 0.4357 | 0.2359 | 0.0013 | 9 |
| 2 | 0.6 | 4 | 0.36 | 1.2 | 0.5857 | 0.0816 | 0.0002 | 4 |
| 3 | 0.7 | 9 | 0.49 | 2.1 | 0.7357 | 0.0345 | 0.0013 | 1 |
| 4 | 0.9 | 16 | 0.81 | 3.6 | 0.8857 | 0.0002 | 0.0002 | 0 |
| 5 | 1.1 | 25 | 1.21 | 5.5 | 1.0357 | 0.0459 | 0.0041 | 1 |
| 6 | 1.3 | 36 | 1.69 | 7.8 | 1.1857 | 0.1716 | 0.0131 | 4 |
| 7 | 1.2 | 49 | 1.44 | 8.4 | 1.3357 | 0.0988 | 0.0184 | 9 |
| 28 | 6.2 | 140 | 6.16 | 29 | 6.2 | 0.6686 | 0.0386 | 28 |
Значимость коэффициента корреляции определяется по формуле (см. п. VI):
Для оценки значимости коэффициента корреляции используют критерий Стьюдента. По таблице Стьюдента находим Tтабл(n-m-1;α/2) = Tтабл(5;0.025) = 2.571 (двусторонняя критическая область)
1-α (95% - доверительный интервал)
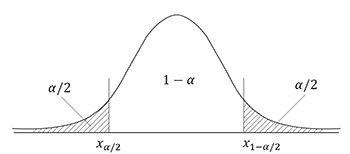
Поскольку Tнабл > Tтабл (наблюдаемое значение критерия Tнабл принадлежит критической области), то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически - значим.
Интервальная оценка для коэффициента корреляции (доверительный интервал).
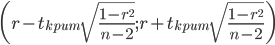
Доверительный интервал для коэффициента корреляции.
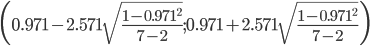
r(0.695;1)
