Эмпирическое корреляционное отношение
Эмпирическое корреляционное отношение измеряет, какую часть общей колеблемости результативного признака вызывает изучаемый фактор. Эмпирическое корреляционное среднее варьирует от 0 до 1.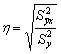
или 
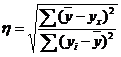
- когда по двум рядам данным X и Y необходимо произвести аналитическую группировку
- группировка уже произведена, необходимо проверить правило сложения дисперсий
- по двум рядам данным X и Y необходимо найти уравнение нелинейной регрессии и оценить его значимость.
Рассмотрим пример однофакторной аналитической группировки.
Таблица - Характеристика зависимости прибыли малых предприятий от оборачиваемости оборотных средств за 1997 г.
| Продолжительность оборота средств, в днях | Число малых предприятий | Середина интервала, дни | Средняя прибыль, млн. руб. | Изменение средней прибыли, млн. руб |
| xi | ni | x'i | yi | yi-yi-1 |
| 20 –30 | 6 | 25 | 14.57 | – |
| 31 – 50 | 8 | 40 | 12.95 | –1.62 |
| 51 – 80 | 6 | 65 | 7.40 | –5.55 |
| Итого | 20 | 43 | 11.77 |
В данном примере:
х– оборачиваемость в днях (фактор);
у– прибыль (результат).
Данные группируются по признаку-фактору. Затем по каждой группе рассчитывается среднее значение. Задача состоит в том, чтобы увидеть, есть связь между признаками или нет; прямая связь или обратная; линейная или нелинейная.
Сопоставим изменения средних значений результата с изменениями фактора. Чтобы эти изменения были сравнимыми, надо делать группировку с равными интервалами или рассчитывать изменения результата на единицу изменения фактора.
В примере средняя прибыль изменяется от группы к группе, следовательно, связь между оборачиваемостью и прибылью есть. Причем обратная: чем медленнее оборачиваются средства, тем меньше прибыль.
Рассчитаем, на сколько снижается прибыль при замедлении оборачиваемости:
1) 
млн. руб./день;
2) 
млн. руб./день.
Полученные значения показывают величину снижения прибыли при замедлении оборачиваемости на 1 день. Здесь: bxy≠const следовательно, связь нелинейная.
bxy – показатели силы связи.
По аналитической группировке измеряют связь при помощи эмпирического корреляционного отношения. Оно основан на правиле разложения дисперсии: общая дисперсия Sy равна сумме внутригрупповой и межгрупповой дисперсий.
Дисперсия внутри группы при относительном постоянстве признака-фактора возникает за счет других факторов (не связанных с изучением). Эта дисперсия называется остаточной
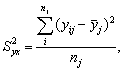
yij – значение признака для i-ой единицы в j-ой группе;
yj – среднее значение признака в j-ой группе;
nj – число единиц в j-ой группе;
m – число групп.
Внутригрупповые дисперсии объединяются в средней величине внутригрупповых дисперсий:
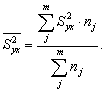
Межгрупповая дисперсия относится на счет изучаемого фактора, она называется факторной
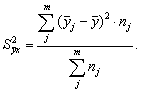
Правило сложения дисперсий
S²y=S²yx+S²y или
Эмпирическое корреляционное отношение измеряет, какую часть общей колеблемости результативного признака вызывает изучаемый фактор. Это отношение факторной дисперсии к общей дисперсии:
– коэффициент детерминации;
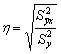– эмпирическое корреляционное отношение.
Рассмотрим пример.
Случай №2.
С целью установления зависимости между урожайностью и сортом винограда в одном из хозяйств на основе выборки определили урожай на 10 кустах винограда.
| Наименование сорта винограда | Число проверенных кустов | Урожай винограда с каждого куста, кг | ||||
| куст№1 | куст №2 | куст№3 | куст №4 | куст№5 | ||
Сорт «А» | 3 | 6 | 5 | 7 | – | – |
Сорт «Б» | 5 | 7 | 6 | 8 | 5 | 9 |
Сорт «В» | 2 | 9 | 7 | – | – | – |
Решение. Если совокупность разбита на группы, то дисперсия признака σ2 может быть определена как сумма межгрупповой дисперсии δ²м.гр. и средней из групповых дисперсий σ²i:
σ²=σ²i+δ²м.гр.
,
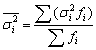где
– дисперсия признака в группе i (групповая дисперсия);
x – индивидуальное значение признака;
xi – среднее значение признака в группе i;
fi – число наблюдений в группе i.
,
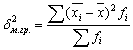где x – среднее значение признака в совокупности.
Отношение межгрупповой дисперсии к общей дает возможность измерить вариацию результативного признака за счет факторного, то есть признака, положенного в основание группировки, и тем самым судить о связи между изучаемыми признаками:
,
где η² – коэффициент детерминации.
Для характеристики тесноты связи берется показатель η – эмпирическое корреляционное отношение, рассчитываемое как
.
Эмпирическое корреляционное среднее варьирует от 0 до 1.
При η=0 связи нет, при η=1 – связь полная.
Применим правило сложения дисперсии к исходным данным.
1. Групповые средние, т.е. средняя урожайность по каждому сорту винограда, равны:
кг;
кг;
кг.
2. Определим среднюю урожайность винограда по хозяйству:
кг.
3. Определим групповую (частную) дисперсию урожайности для каждого сорта отдельно:
;
;
.
4. Средняя из частных дисперсий:
.
5. Межгрупповая дисперсия:
.
6. Определяем общую дисперсию урожайности по всей совокупности, используя правило сложения дисперсий:
σ2 = 1,4 + 0,49 = 1,89
Проверим этот вывод путем расчета общей дисперсии обычным способом:
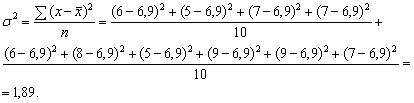
7. Определим коэффициент детерминации – η²:
или 26%.
Таким образом, только на 26% вариация урожайности обусловлена различиями между сортами, а на 74% – другими факторами (характером почвы, удобренностью участков, поливом и т.п.).
8. Определяем эмпирическое корреляционное отношение:
.
Следовательно, можно утверждать, что связь умеренная.
Случай №1.
Используя вторичные источники данных, проведем выборочное наблюдение 30 предлагаемых на продажу автомобилей Kia Sorento за последние три месяца.
Исследуемые признаки: Y – цена автомобиля, тыс. руб.; Х1 – время эксплуатации, лет;
Решение:
Данные группируются по признаку-фактору. Затем по каждой группе рассчитывается среднее значение. Задача состоит в том, чтобы увидеть, есть связь между признаками или нет; прямая связь или обратная; линейная или нелинейная.
Тогда ширина интервала составит:
Для каждого значения ряда подсчитаем, какое количество раз оно попадает в тот или иной интервал. Для этого сортируем ряд по возрастанию.
| 470 | 470 - 563 | 1 |
| 470 | 470 - 563 | 2 |
| 470 | 470 - 563 | 3 |
| 480 | 470 - 563 | 4 |
| 480 | 470 - 563 | 5 |
| 485 | 470 - 563 | 6 |
| 485 | 470 - 563 | 7 |
| 500 | 470 - 563 | 8 |
| 525 | 470 - 563 | 9 |
| 530 | 470 - 563 | 10 |
| 530 | 470 - 563 | 11 |
| 550 | 470 - 563 | 12 |
| 560 | 470 - 563 | 13 |
| 590 | 563 - 656 | 1 |
| 599 | 563 - 656 | 2 |
| 600 | 563 - 656 | 3 |
| 600 | 563 - 656 | 4 |
| 600 | 563 - 656 | 5 |
| 640 | 563 - 656 | 6 |
| 640 | 563 - 656 | 7 |
| 640 | 563 - 656 | 8 |
| 655 | 563 - 656 | 9 |
| 680 | 656 - 749 | 1 |
| 695 | 656 - 749 | 2 |
| 700 | 656 - 749 | 3 |
| 700 | 656 - 749 | 4 |
| 705 | 656 - 749 | 5 |
| 710 | 656 - 749 | 6 |
| 729 | 656 - 749 | 7 |
| 749 | 656 - 749 | 8 |
Аналитическая группировка.
| Группы | № | Кол-во, f | ∑X | X= ∑X / f | ∑Y | Y= ∑Y / f |
| 470 - 563 | 1,2,3,4,5,6,7,8,9,10,11,12,13 | 13 | 6535 | 502.69 | 121 | 9.31 |
| 563 - 656 | 14,15,16,17,18,19,20,21,22 | 9 | 5564 | 618.22 | 67 | 7.44 |
| 656 - 749 | 23,24,25,26,27,28,29,30 | 8 | 5668 | 708.5 | 43 | 5.38 |
| Итого | 30 | 17767 | 231 |
1. Находим средние значения каждой группы.
Общее средние значение для всей совокупности:
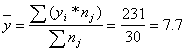
2. Дисперсия внутри группы при относительном постоянстве признака-фактора возникает за счет других факторов (не связанных с изучением). Эта дисперсия называется остаточной:
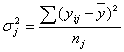
Расчет для группы: 470 - 563(1,2,3,4,5,6,7,8,9,10,11,12,13)
| yj | (yj- yср)2 | Результат |
| 11 | (11 - 9.31)2 | 2.86 |
| 11 | (11 - 9.31)2 | 2.86 |
| 11 | (11 - 9.31)2 | 2.86 |
| 10 | (10 - 9.31)2 | 0.48 |
| 11 | (11 - 9.31)2 | 2.86 |
| 9 | (9 - 9.31)2 | 0.0947 |
| 6 | (6 - 9.31)2 | 10.94 |
| 9 | (9 - 9.31)2 | 0.0947 |
| 11 | (11 - 9.31)2 | 2.86 |
| 6 | (6 - 9.31)2 | 10.94 |
| 8 | (8 - 9.31)2 | 1.71 |
| 8 | (8 - 9.31)2 | 1.71 |
| 10 | (10 - 9.31)2 | 0.48 |
| Итого | 40.77 |
Расчет для группы: 563 - 656(14,15,16,17,18,19,20,21,22)
| yj | (yj- yср)2 | Результат |
| 9 | (9 - 7.44)2 | 2.42 |
| 7 | (7 - 7.44)2 | 0.2 |
| 7 | (7 - 7.44)2 | 0.2 |
| 8 | (8 - 7.44)2 | 0.31 |
| 9 | (9 - 7.44)2 | 2.42 |
| 6 | (6 - 7.44)2 | 2.09 |
| 5 | (5 - 7.44)2 | 5.98 |
| 8 | (8 - 7.44)2 | 0.31 |
| 8 | (8 - 7.44)2 | 0.31 |
| Итого | 14.22 |
Расчет для группы: 656 - 749(23,24,25,26,27,28,29,30)
| yj | (yj- yср)2 | Результат |
| 6 | (6 - 5.38)2 | 0.39 |
| 5 | (5 - 5.38)2 | 0.14 |
| 6 | (6 - 5.38)2 | 0.39 |
| 5 | (5 - 5.38)2 | 0.14 |
| 5 | (5 - 5.38)2 | 0.14 |
| 6 | (6 - 5.38)2 | 0.39 |
| 5 | (5 - 5.38)2 | 0.14 |
| 5 | (5 - 5.38)2 | 0.14 |
| Итого | 1.88 |
3. Внутригрупповые дисперсии объединяются в средней величине внутригрупповых дисперсий:
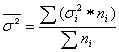
Средняя из частных дисперсий:
4. Межгрупповая дисперсияотносится на счет изучаемого фактора, она называется факторной
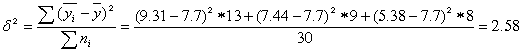
Определяем общую дисперсию по всей совокупности, используя правило сложения дисперсий:
σ²=σ²i+δ²
σ2= 1.9 + 2.58 = 4.48
Проверим этот вывод путем расчета общей дисперсии обычным способом:
| yi | (yi- yср)2 | Результат |
| 11 | (11 - 7.7)2 | 10.89 |
| 11 | (11 - 7.7)2 | 10.89 |
| 11 | (11 - 7.7)2 | 10.89 |
| 10 | (10 - 7.7)2 | 5.29 |
| 11 | (11 - 7.7)2 | 10.89 |
| 9 | (9 - 7.7)2 | 1.69 |
| 6 | (6 - 7.7)2 | 2.89 |
| 9 | (9 - 7.7)2 | 1.69 |
| 11 | (11 - 7.7)2 | 10.89 |
| 6 | (6 - 7.7)2 | 2.89 |
| 8 | (8 - 7.7)2 | 0.09 |
| 8 | (8 - 7.7)2 | 0.09 |
| 10 | (10 - 7.7)2 | 5.29 |
| 9 | (9 - 7.7)2 | 1.69 |
| 7 | (7 - 7.7)2 | 0.49 |
| 7 | (7 - 7.7)2 | 0.49 |
| 8 | (8 - 7.7)2 | 0.09 |
| 9 | (9 - 7.7)2 | 1.69 |
| 6 | (6 - 7.7)2 | 2.89 |
| 5 | (5 - 7.7)2 | 7.29 |
| 8 | (8 - 7.7)2 | 0.09 |
| 8 | (8 - 7.7)2 | 0.09 |
| 6 | (6 - 7.7)2 | 2.89 |
| 5 | (5 - 7.7)2 | 7.29 |
| 6 | (6 - 7.7)2 | 2.89 |
| 5 | (5 - 7.7)2 | 7.29 |
| 5 | (5 - 7.7)2 | 7.29 |
| 6 | (6 - 7.7)2 | 2.89 |
| 5 | (5 - 7.7)2 | 7.29 |
| 5 | (5 - 7.7)2 | 7.29 |
| Итого | 134.3 |
Определяем эмпирическое корреляционное отношение:
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < η < 0.3: слабая;
0.3 < η < 0.5: умеренная;
0.5 < η < 0.7: заметная;
0.7 < η < 0.9: высокая;
0.9 < η < 1: весьма высокая;
В нашем примере связь между признаком Y фактором X высокая
Определим коэффициент детерминации:
Таким образом, на 57.66% вариация обусловлена различиями между признаками, а на 42.34% – другими факторами.
Перейти к онлайн решению своей задачи
Случай №3. Подобные задачи можно решить с помощью сервиса парное уравнение регрессии.
Рассмотрим исходные данные предыдущего примера. На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер.
Линейное уравнение регрессии имеет вид y = bx + a + ε
Система нормальных уравнений.
a•n + b∑x = ∑y
a∑x + b∑x2 = ∑y•x
Для наших данных система уравнений имеет вид
30a + 231 b = 17767
231 a + 1913 b = 132293
Из первого уравнения выражаем а и подставим во второе уравнение:
Получаем эмпирические коэффициенты регрессии: b = -33.6031, a = 850.9774
Уравнение регрессии (эмпирическое уравнение регрессии):
y = -33.6031 x + 850.9774
Для расчета параметров регрессии построим расчетную таблицу (табл. 1)
| x | y | x2 | y2 | x·y |
| 11 | 470 | 121 | 220900 | 5170 |
| 11 | 470 | 121 | 220900 | 5170 |
| 11 | 470 | 121 | 220900 | 5170 |
| 10 | 480 | 100 | 230400 | 4800 |
| 11 | 480 | 121 | 230400 | 5280 |
| 9 | 485 | 81 | 235225 | 4365 |
| 6 | 485 | 36 | 235225 | 2910 |
| 9 | 500 | 81 | 250000 | 4500 |
| 11 | 525 | 121 | 275625 | 5775 |
| 6 | 530 | 36 | 280900 | 3180 |
| 8 | 530 | 64 | 280900 | 4240 |
| 8 | 550 | 64 | 302500 | 4400 |
| 10 | 560 | 100 | 313600 | 5600 |
| 9 | 590 | 81 | 348100 | 5310 |
| 7 | 599 | 49 | 358801 | 4193 |
| 7 | 600 | 49 | 360000 | 4200 |
| 8 | 600 | 64 | 360000 | 4800 |
| 9 | 600 | 81 | 360000 | 5400 |
| 6 | 640 | 36 | 409600 | 3840 |
| 5 | 640 | 25 | 409600 | 3200 |
| 8 | 640 | 64 | 409600 | 5120 |
| 8 | 655 | 64 | 429025 | 5240 |
| 6 | 680 | 36 | 462400 | 4080 |
| 5 | 695 | 25 | 483025 | 3475 |
| 6 | 700 | 36 | 490000 | 4200 |
| 5 | 700 | 25 | 490000 | 3500 |
| 5 | 705 | 25 | 497025 | 3525 |
| 6 | 710 | 36 | 504100 | 4260 |
| 5 | 729 | 25 | 531441 | 3645 |
| 5 | 749 | 25 | 561001 | 3745 |
| 231 | 17767 | 1913 | 10761193 | 132293 |
1. Параметры уравнения регрессии.
Выборочные средние.
Выборочные дисперсии:
Среднеквадратическое отклонение
1.1. Коэффициент корреляции
Ковариация.
cov(x,y)=x·y-x·y = 4409.77-7.7·592.23 = -150.43
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:
Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < rxy < 0.3: слабая;
0.3 < rxy < 0.5: умеренная;
0.5 < rxy < 0.7: заметная;
0.7 < rxy < 0.9: высокая;
0.9 < rxy < 1: весьма высокая;
В нашем примере связь между признаком Y фактором X высокая и обратная.
Эмпирическое корреляционное отношение.
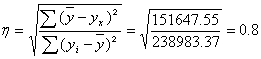
где (y-y(x))²=238983.37-87335.81=151647.55
Теоретическое корреляционное отношение для линейной связи равно коэффициенту корреляции rxy.
Коэффициент детерминации.
R2= -0.82 = 0.63, т.е. в 63.46 % случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - средняя. Остальные 36.54 % изменения Y объясняются факторами, не учтенными в модели.
Для оценки качества параметров регрессии построим расчетную таблицу (табл. 2)
| x | y | y(x) | (yi-y)2 | (y-y(x))2 |
| 11 | 470 | 481.34 | 14940.99 | 128.66 |
| 11 | 470 | 481.34 | 14940.99 | 128.66 |
| 11 | 470 | 481.34 | 14940.99 | 128.66 |
| 10 | 480 | 514.95 | 12596.32 | 1221.23 |
| 11 | 480 | 481.34 | 12596.32 | 1.8 |
| 9 | 485 | 548.55 | 11498.99 | 4038.51 |
| 6 | 485 | 649.36 | 11498.99 | 27013.77 |
| 9 | 500 | 548.55 | 8506.99 | 2357.03 |
| 11 | 525 | 481.34 | 4520.32 | 1905.93 |
| 6 | 530 | 649.36 | 3872.99 | 14246.49 |
| 8 | 530 | 582.15 | 3872.99 | 2719.87 |
| 8 | 550 | 582.15 | 1783.65 | 1033.78 |
| 10 | 560 | 514.95 | 1038.99 | 2029.85 |
| 9 | 590 | 548.55 | 4.99 | 1718.16 |
| 7 | 599 | 615.76 | 45.79 | 280.75 |
| 7 | 600 | 615.76 | 60.32 | 248.24 |
| 8 | 600 | 582.15 | 60.32 | 318.54 |
| 9 | 600 | 548.55 | 60.32 | 2647.18 |
| 6 | 640 | 649.36 | 2281.65 | 87.58 |
| 5 | 640 | 682.96 | 2281.65 | 1845.71 |
| 8 | 640 | 582.15 | 2281.65 | 3346.35 |
| 8 | 655 | 582.15 | 3939.65 | 5306.77 |
| 6 | 680 | 649.36 | 7702.99 | 938.89 |
| 5 | 695 | 682.96 | 10560.99 | 144.92 |
| 6 | 700 | 649.36 | 11613.65 | 2564.55 |
| 5 | 700 | 682.96 | 11613.65 | 290.3 |
| 5 | 705 | 682.96 | 12716.32 | 485.68 |
| 6 | 710 | 649.36 | 13868.99 | 3677.37 |
| 5 | 729 | 682.96 | 18705.12 | 2119.52 |
| 5 | 749 | 682.96 | 24575.79 | 4361.05 |
| 231 | 17767 | 17767 | 238983.37 | 87335.81 |