Двухфакторный дисперсионный анализ
В двухфакторном дисперсионном анализе проверяется гипотеза о равенстве математических ожиданий выходного контролируемого параметра y при различных уровнях двух факторов.Назначение сервиса. С помощью онлайн-калькулятора можно:
- провести двухфакторный дисперсионный анализ (см. также одномерный дисперсионный анализ);
- ответить на вопрос - совпадают или нет средние значения экспериментов, влияют ли факторы на результат;
- при выбранном уровне значимости подтвердить или опровергнуть нулевую гипотезу H0 о равенстве групповых средних и дисперсий (по критерию Кохрена);
При применении двухфакторного дисперсионного анализа исследователь проверяет влияние двух независимых переменных (факторов) на зависимую переменную. Может быть изучен также эффект взаимодействия двух переменных.
Исследуемые группы называют эффектами обработки. Схема двухфакторного дисперсионного анализа имеет несколько нулевых гипотез: одна для каждой независимой переменной и одна для взаимодействия.
Условия применения двухмерного дисперсионного анализа:
- Генеральные совокупности, из которых извлечены выборки, должны быть нормально распределены.
- Выборки должны быть независимыми.
- Дисперсии генеральных совокупностей, из которых извлекались выборки, должны быть равными.
- Группы должны иметь одинаковый объем выборки.
| Сумма квадратов | df | Среднее квадратичное | F | |
| Фактор A | SSA | m-1 | MSA | FA |
| Фактор B | SSB | k-1 | MSB | FB |
| Взаимодействие, AxB | SSAB | (m-1)(k-1) | MSAB | FAB |
| Ошибка | SSerror | m*k(n-1) | MSerror | |
| ИТОГО |
SSA сумма квадратов для фактора А
SSB - сумма квадратов для фактора В
SSAxB - сумма квадратов для взаимодействия факторов
SSerror - сумма квадратов для ошибки
m- количество уровней фактора А
k- количество уровней фактора В
n- количество объектов в каждой группе
Пример. В химической лаборатории проверяется влияние температуры (фактор А) и катализатора (фактор В) на выход продукта химического синтеза. Полученные результаты приведены в таблице. Проведите двухфакторный дисперсионный анализ. При уровне значимости a = 0,05 проверьте гипотезу о влиянии факторов А и В и их комбинации на указанный признак. Предварительно проверьте по критерию Кочрена равенство дисперсий в группах.
| В1 | В2 | В3 | |
| А1 | 16; 19; 17; 16 | 18; 16; 17; 14 | 16; 16; 18; 13 |
| А2 | 22; 22; 19; 23 | 18; 19; 23; 24 | 18; 16; 19; 20 |
| А3 | 20; 16; 18; 19 | 18; 17; 19; 19 | 20; 20; 16; 16 |
| А4 | 23; 20; 22; 23 | 19; 18; 19; 22 | 20; 19; 20; 22 |
Решение.
Шаг №1. Формулировка гипотез.
Гипотезы для взаимодействия:
Н0: Фактор A (температура) и фактор B (катализатор) не оказывают эффекта взаимодействия на результат Y (продукт химического синтеза).
Н1: Фактор A и фактор B оказывают эффекта взаимодействия на результат Y.
Гипотезы для фактора A:
Н0: Для всех режимов температуры Ai нет разницы между средним результатом продукта химического синтеза Y.
Н1: Для всех типов Ai существует разница между средним результатом Y.
Гипотезы для фактора B:
Н0: Для всех типов катализатора Bj нет разницы между средним результатом Y.
Н1: Для всех типов Bj существует разница между средним результатом Y.
Шаг №2. Расчет данных.
Фактор А принимает m = 4 различных значений.
Фактор B принимает k = 3 различных значений.
На каждом из сочетаний уровней имеется n = 4 наблюдений выходной величины.
Расчет средних.
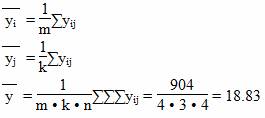
| yi1 | yi2 | yi3 | yi | |
| y1j | 17 | 16.25 | 15.75 | 16.33 |
| y2j | 21.5 | 21 | 18.25 | 20.25 |
| y3j | 18.25 | 18.25 | 18 | 18.17 |
| y4j | 22 | 19.5 | 20.25 | 20.58 |
| yj | 19.69 | 18.75 | 18.06 | y = 18.83 |
Сумма квадратов отклонений под влиянием m уровней фактора А:
Сумма квадратов отклонений под влиянием k уровней фактора B:
Сумма квадратов отклонений взаимодействия факторов A и B:
Остаточная сумма квадратов:
Оценка дисперсии уровней A (влияние фактора A на продукт химического синтеза):
Оценка дисперсии уровней B (влияние фактора B на продукт химического синтеза):
Наличие двух факторов позволяет использовать еще одну оценку дисперсии – взаимодействия:
Оценка дисперсии ошибки (учитывает влияние всех факторов, в том числе и не учтенных):
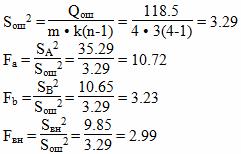
Шаг №3. Анализ результатов.
Степени свободы для каждого фактора:
Фактор А: v1 = m-1 = 4 - 1 = 3
Фактор B: v2 = k-1 = 3 - 1 = 2
Взаимодействие(AxB): v3 = (m-1)(k-1) = (4-1)(3 - 1) = 6
Ошибка внутри группы: vош = m • k(n-1) = 4 • 3(4-1) = 36
| SS | df | MS | F | |
Фактор A | 35.29 | 3 | 35.29 | 10.72 |
Фактор B | 5.32 | 2 | 10.65 | 3.23 |
Взаимодействие A и B | 4.93 | 6 | 9.85 | 2.99 |
Ошибка внутри группы | 118.5 | 36 | 3.29 | |
Итого | 164.04 | 47 |
Табличное значение критерия со степенями свободы v1=3 и v2=36, Fтабл = 2.84
10.722 > Fтабл, следовательно, данные противоречат гипотезе H0, и следует считать, что режимы температуры оказывают влияния на средний результат химического синтеза.
Табличное значение критерия со степенями свободы v1=2 и v2=36, Fтабл = 3.23
3.234 > Fтабл, следовательно, данные противоречат гипотезе H0, и следует считать, что типы катализаторов оказывают влияния на средний результат химического синтеза.
Табличное значение критерия со степенями свободы v1=6 и v2=36, Fтабл = 2.34
2.994 > Fтабл, следовательно, данные противоречат гипотезе H0, и следует считать, что уровни факторов A и B оказывают влияния на средний результат y.
Поскольку нулевая гипотеза об эффекте взаимодействия была отвергнута, можно сделать вывод о том, что сочетание температуры и катализаторов оказывает существенное влияние на продукт химического синтеза.
Критерий Кохрена используется для оценки однородности (отсутствия выбросов) дисперсий результатов испытаний. Расчетное значение критерия Кохрена находится по формуле:
где Smax - наибольшее значение среднего квадратического отклонения в одной из всех анализируемых групп; Si - среднее квадратическое отклонение результатов испытаний в группах, определяемое по формуле:
где
ni - число результатов измерений в i-ой группе на данном уровне;
yik - k-ый из этих результатов измерений;
y - среднее арифметическое значение результатов измерений в i-ой группе.
Рассчитаем показатели разброса (расхождения) в базовых элементах:
| 6 | 8.75 | 12.75 |
| 9 | 26 | 8.75 |
| 8.75 | 2.75 | 16 |
| 6 | 9 | 4.75 |
Максимальным из них является Smax2 = 26
Критерий Кохрана:
Находим по таблице "Критические значения для критерия Кохрана": Gкр(p;n-1;m*k) = G(0.05;3;12) = 0.3264
Так как 0.22 ≤ Gкр, можно сделать вывод, что дисперсий в группах равны (гипотеза о равенстве дисперсий принимается - опыты считаются воспроизводимыми, а оценки дисперсий однородными).



