Коэффициент ранговой корреляции Кендалла
Ранговый коэффициент корреляции характеризует общий характер нелинейной зависимости: возрастание или убывание результативного признака при возрастании факторного. Это показатель тесноты монотонной нелинейной связи.Назначение сервиса. С помощью данного онлайн-калькулятора производится расчет коэффициента ранговой корреляции Кендэла по всем основным формулам, а также оценка его значимости.
Предложенный Кендэлом коэффициент строится на основе отношений типа «больше –меньше», справедливость которых установлена при построении шкал.
Выделим пару объектов и сравним их ранги по одному признаку и по другому. Если по данному признаку ранги образуют прямой порядок (т.е. порядок натурального ряда), то паре приписывается +1, если обратный, то –1. Для выделенной пары соответствующие плюс – минус единицы (по признаку X и по признаку Y) перемножаются. Результат, очевидно, равен +1; если ранги пары обоих признаков расположены в одинаковой последовательности, и –1, если в обратной.
Если порядки рангов по обоим признакам у всех пар одинаковы, то сумма единиц, приписанных всем парам объектов, максимальна и равна числу пар. Если порядки рангов всех пар обратны, то –C2N. В общем случае C2N = P + Q, где P – число положительных, а Q – отрицательных единиц, приписанных парам при сопоставлении их рангов по обоим признакам.
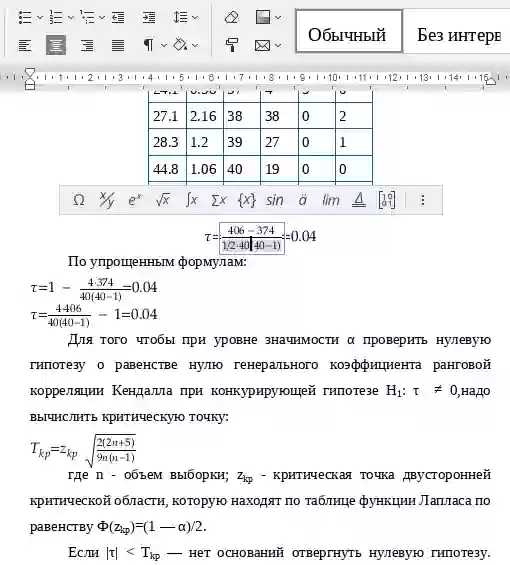
Величина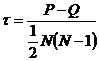 
называется коэффициентом Кендалла.
Из формулы видно, что коэффициент τ представляет собой разность доли пар объектов, у которых совпадает порядок по обоим признакам (по отношению к числу всех пар) 
и доли пар объектов, у которых порядок не совпадает 
.
Например, значение коэффициента 0,60 означает, что у 80% пар порядок объектов совпадает, а у 20% не совпадает (80% + 20% = 100%; 0,80 – 0,20 = 0,60). Т.е. τ можно трактовать как разность вероятностей совпадения и не совпадения порядков по обоим признакам для наугад выбранной пары объектов.
В общем случае расчет τ (точнее Р или Q) даже для N порядка 10 оказывается громоздким.
Покажем, как упростить вычисления.
Пример. Зависимость между объемом промышленной продукции и инвестициями в основной капитал по 10 областям одного из федеральных округов РФ в 2003 году характеризуется следующими данными:
| Область | Объем промышленной продукции, млрд руб. | Инвестиции в основной капитал, млрд руб. |
| Белгородская | 64,6 | 10,22 |
| Брянская | 21,5 | 4,12 |
| Владимирская | 51,1 | 8,58 |
| Воронежская | 54,4 | 14,79 |
| Ивановская | 20,6 | 2,88 |
| Калужская | 35,7 | 7,24 |
| Костромская | 18,4 | 5,57 |
| Курская | 37,1 | 9,67 |
| Липецкая | 90,6 | 10,45 |
| Смоленская | 39,8 | 10,48 |
Вычислите ранговые коэффициенты корреляции Спирмена и Кендэла. Проверить их значимость при α=0,05. Сформулируйте вывод о зависимости между объемом промышленной продукции и инвестициями в основной капитал по рассматриваемым областям РФ.
Решение. Присвоим ранги признаку Y и фактору X.
Расположим объекты так, чтобы их ранги по X представили натуральный ряд. Так как оценки, приписываемые каждой паре этого ряда, положительные, значения «+1», входящие в Р, будут порождаться только теми парами, ранги которых по Y образуют прямой порядок.
Их легко подсчитать, сопоставляя последовательно ранги каждого объекта в ряду Y с стальными.
Упорядочим данные по X.
В ряду Y справа от 3 расположено 7 рангов, превосходящих 3, следовательно, 3 породит в Р слагаемое 7.
Справа от 1 стоят 8 ранга, превосходящих 1 (это 2, 4, 6, 9, 5, 10, 7, 8), т.е. в Р войдет 8 и т.д. В итоге Р = 37 и с использованием формул имеем:
| X | Y | ранг X, dx | ранг Y, dy | P | Q |
| 18.4 | 5.57 | 1 | 3 | 7 | 2 |
| 20.6 | 2.88 | 2 | 1 | 8 | 0 |
| 21.5 | 4.12 | 3 | 2 | 7 | 0 |
| 35.7 | 7.24 | 4 | 4 | 6 | 0 |
| 37.1 | 9.67 | 5 | 6 | 4 | 1 |
| 39.8 | 10.48 | 6 | 9 | 1 | 3 |
| 51.1 | 8.58 | 7 | 5 | 3 | 0 |
| 54.4 | 14.79 | 8 | 10 | 0 | 2 |
| 64.6 | 10.22 | 9 | 7 | 1 | 0 |
| 90.6 | 10.45 | 10 | 8 | 0 | 0 |
| 37 | 8 |
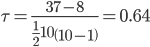
По упрощенным формулам:
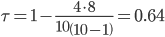
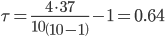
Для того чтобы при уровне значимости α проверить нулевую гипотезу о равенстве нулю генерального коэффициента ранговой корреляции Кендалла при конкурирующей гипотезе Н1: τ ≠ 0,надо вычислить критическую точку:
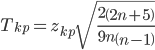
где n - объем выборки; zkp - критическая точка двусторонней критической области, которую находят по таблице функции Лапласа по равенству Ф(zkp)=(1—α)/2.
Если |τ| < Tkp — нет оснований отвергнуть нулевую гипотезу. Ранговая корреляционная связь между качественными признаками незначима. Если |τ| > Tkp — нулевую гипотезу отвергают. Между качественными признаками существует значимая ранговая корреляционная связь.
Найдем критическую точку zkp
Ф(zkp) = (1-α)/2 = (1 - 0.05)/2 = 0.475
По таблице Лапласа находим zkp = 1.96
Найдем критическую точку:
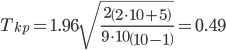
Так как τ > Tkp — отвергаем нулевую гипотезу; ранговая корреляционная связь между оценками по двум тестам значимая.
Пример. По данным об объеме строительно-монтажных работ, выполненных собственными силами, и численности работающих в 10 строительных компаниях одного из городов РФ, определить зависимость между этими признаками с помощью коэффициента Кендела.
Решение находим с помощью калькулятора.
Присвоим ранги признаку Y и фактору X.
Расположим объекты так, чтобы их ранги по X представили натуральный ряд. Так как оценки, приписываемые каждой паре этого ряда, положительные, значения «+1», входящие в Р, будут порождаться только теми парами, ранги которых по Y образуют прямой порядок.
Их легко подсчитать, сопоставляя последовательно ранги каждого объекта в ряду Y с стальными.
Коэффициент Кендэла.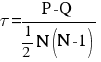
В общем случае расчет τ (точнее Р или Q) даже для N порядка 10 оказывается громоздким. Покажем, как упростить вычисления.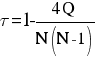
или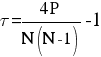
Решение.
Упорядочим данные по X.
В ряду Y справа от 2 расположено 8 рангов, превосходящих 2, следовательно, 2 породит в Р слагаемое 8.
Справа от 4 стоят 6 ранга, превосходящих 4 (это 7, 5, 6, 8, 9, 10), т.е. в Р войдет 6 и т.д. В итоге Р = 29 и с использованием формул имеем:
| X | Y | ранг X, dx | ранг Y, dy | P | Q |
| 38 | 292 | 1 | 2 | 8 | 1 |
| 50 | 302 | 2 | 4 | 6 | 2 |
| 52 | 366 | 3 | 7 | 3 | 4 |
| 54 | 312 | 4 | 5 | 4 | 2 |
| 59 | 359 | 5 | 6 | 3 | 2 |
| 61 | 398 | 6 | 8 | 2 | 2 |
| 66 | 401 | 7 | 9 | 1 | 2 |
| 70 | 298 | 8 | 3 | 1 | 1 |
| 71 | 283 | 9 | 1 | 1 | 0 |
| 73 | 413 | 10 | 10 | 0 | 0 |
| 29 | 16 |
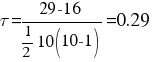
По упрощенным формулам:
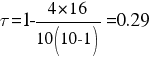
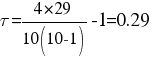
Для того чтобы при уровне значимости α проверить нулевую гипотезу о равенстве нулю генерального коэффициента ранговой корреляции Кендалла при конкурирующей гипотезе Н1: τ ≠ 0,надо вычислить критическую точку:
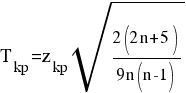
где n - объем выборки; zkp - критическая точка двусторонней критической области, которую находят по таблице функции Лапласа по равенству Ф(zkp)=(1 — α)/2.
Если |τ| < Tkp — нет оснований отвергнуть нулевую гипотезу. Ранговая корреляционная связь между качественными признаками незначима. Если |τ| > Tkp — нулевую гипотезу отвергают. Между качественными признаками существует значимая ранговая корреляционная связь.
Найдем критическую точку zkp
Ф(zkp) = (1 - α)/2 = (1 - 0.05)/2 = 0.475
По таблице Лапласа находим zkp = 1.96
Найдем критическую точку:
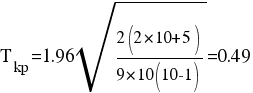
Так как τ < Tkp — принимаем нулевую гипотезу; ранговая корреляционная связь между оценками по двум тестам незначимая