Средняя ошибка аппроксимации
Средняя ошибка аппроксимации - среднее отклонение расчетных значений от фактических:Относительная ошибка аппроксимации
По семи территориям Уральского района за 199Х г. известны значения двух признаков.
| Район | Расходы на покупку продовольственных товаров в общих расходах, %, у | Среднедневная заработная плата одного работающего, руб., х |
| Удмуртская респ. | 68,8 | 45,1 |
| Свердловская обл. | 61,2 | 59,0 |
| Башкортостан | 59,9 | 57,2 |
| Челябинская обл. | 56,7 | 61,8 |
| Пермская обл. | 55,0 | 58,8 |
| Курганская обл. | 54,3 | 47,2 |
| Оренбургская обл. | 49,3 | 55,2 |
1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
а) линейной;
б) степенной;
в) показательной;
г) равносторонней гиперболы (так же нужно придумать как предварительно линеаризовать данную модель).
2. Оценить каждую модель через среднюю ошибку аппроксимации Аср и F-критерий Фишера.
Перейти к онлайн решению своей задачи
Решение проводим при помощь онлайн калькулятора Линейное уравнение регрессии.
а) линейное уравнение регрессии;
Использование графического метода.
Этот метод применяют для наглядного изображения формы связи между изучаемыми экономическими показателями. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают индивидуальные значения результативного признака Y, а по оси абсцисс - индивидуальные значения факторного признака X.
Совокупность точек результативного и факторного признаков называется полем корреляции.
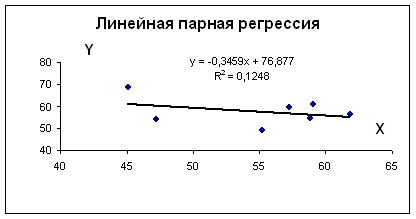
На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер.
Линейное уравнение регрессии имеет вид y = bx + a + ε
Здесь ε - случайная ошибка (отклонение, возмущение).
Причины существования случайной ошибки:
1. Невключение в регрессионную модель значимых объясняющих переменных;
2. Агрегирование переменных. Например, функция суммарного потребления – это попытка общего выражения совокупности решений отдельных индивидов о расходах. Это лишь аппроксимация отдельных соотношений, которые имеют разные параметры.
3. Неправильное описание структуры модели;
4. Неправильная функциональная спецификация;
5. Ошибки измерения.
Так как отклонения εi для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то:
1) по наблюдениям xi и yi можно получить только оценки параметров α и β
2) Оценками параметров α и β регрессионной модели являются соответственно величины а и b, которые носят случайный характер, т.к. соответствуют случайной выборке;
Тогда оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где ei – наблюдаемые значения (оценки) ошибок εi, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Для оценки параметров α и β - используют МНК (метод наименьших квадратов).
Система нормальных уравнений.
Для наших данных система уравнений имеет вид
Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = -0.35, a = 76.88
Уравнение регрессии: y = -0.35 x + 76.88
| x | y | x 2 | y 2 | x • y | y(x) | (yi-ycp) 2 | (y-y(x))2 | |y - yx|:y |
| 45,1 | 68,8 | 2034,01 | 4733,44 | 3102,88 | 61,28 | 119,12 | 56,61 | 0,1094 |
| 59 | 61,2 | 3481 | 3745,44 | 3610,8 | 56,47 | 10,98 | 22,4 | 0,0773 |
| 57,2 | 59,9 | 3271,84 | 3588,01 | 3426,28 | 57,09 | 4,06 | 7,9 | 0,0469 |
| 61,8 | 56,7 | 3819,24 | 3214,89 | 3504,06 | 55,5 | 1,41 | 1,44 | 0,0212 |
| 58,8 | 55 | 3457,44 | 3025 | 3234 | 56,54 | 8,33 | 2,36 | 0,0279 |
| 47,2 | 54,3 | 2227,84 | 2948,49 | 2562,96 | 60,55 | 12,86 | 39,05 | 0,1151 |
| 55,2 | 49,3 | 3047,04 | 2430,49 | 2721,36 | 57,78 | 73,71 | 71,94 | 0,172 |
| 384,3 | 405,2 | 21338,41 | 23685,76 | 22162,34 | 405,2 | 230,47 | 201,71 | 0,5699 |
Примечание: значения y(x) находятся из полученного уравнения регрессии:
y(45.1) = -0.35*45.1 + 76.88 = 61.28
y(59) = -0.35*59 + 76.88 = 56.47
... ... ...
Ошибка аппроксимации
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации. Средняя ошибка аппроксимации - среднее отклонение расчетных значений от фактических:
F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R2=0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=5, Fkp = 6.61
Поскольку фактическое значение F < Fkp, то коэффициент детерминации статистически не значим (Найденная оценка уравнения регрессии статистически не надежна).
б) степенная регрессия;
Решение проводится с помощью сервиса Нелинейная регрессия. При выборе укажите Степенная y = axb
в) показательная регрессия;
г) модель равносторонней гиперболы.
Система нормальных уравнений.
Для наших данных система уравнений имеет вид
7a + 0.1291b = 405.2
0.1291a + 0.0024b = 7.51
Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = 1054.67, a = 38.44
Уравнение регрессии:
y = 1054.67 / x + 38.44
Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.
Поскольку ошибка меньше 15%, то данное уравнение можно использовать в качестве регрессии.
|
1/x |
y |
x 2 |
y 2 |
x • y |
y(x) |
(yi-ycp) 2 |
(y-y(x))2 |
|y - yx|:y |
|
0.0222 |
68.8 |
0.0005 |
4733.44 |
1.53 |
61.82 |
119.12 |
48.71 |
0.1014 |
|
0.0169 |
61.2 |
0.0003 |
3745.44 |
1.04 |
56.31 |
10.98 |
23.9 |
0.0799 |
|
0.0175 |
59.9 |
0.0003 |
3588.01 |
1.05 |
56.87 |
4.06 |
9.16 |
0.0505 |
|
0.0162 |
56.7 |
0.0003 |
3214.89 |
0.9175 |
55.5 |
1.41 |
1.44 |
0.0211 |
|
0.017 |
55 |
0.0003 |
3025 |
0.9354 |
56.37 |
8.33 |
1.88 |
0.0249 |
|
0.0212 |
54.3 |
0.0004 |
2948.49 |
1.15 |
60.78 |
12.86 |
41.99 |
0.1193 |
|
0.0181 |
49.3 |
0.0003 |
2430.49 |
0.8931 |
57.54 |
73.71 |
67.93 |
0.1672 |
|
0.1291 |
405.2 |
0.0024 |
23685.76 |
7.51 |
405.2 |
230.47 |
195.01 |
0.5645 |
Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R2=0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
Табличное значение критерия со степенями свободы k1=1 и k2=5, Fkp = 6.61
Поскольку фактическое значение F < Fkp, то коэффициент детерминации статистически не значим (Найденная оценка уравнения регрессии статистически не надежна).


