Индекс корреляции

Индекс корреляции - нормированный показатель тесноты связи. Для линейной связи его значение равно коэффициенту корреляции.
Для нелинейных регрессионных моделей его значение используется для оценки значимости этих моделей по критерию Фишера.

$Индекс корреляции: формула$

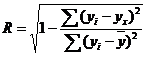
Пример. Найдем степенное уравнение регрессии y = ax^b.
Приводим к линейной системе уравнений:
ln(y) = ln(a) + bln(x)
Система нормальных уравнений.
a•n + b∑x = ∑y
a∑x + b∑x² = ∑y•x
Для наших данных система уравнений имеет вид
28a + 314 b = 231
314 a + 3601.3 b = 2651
Из первого уравнения выражаем а и подставим во второе уравнение:
Получаем эмпирические коэффициенты регрессии: b = 0.77, a = 0.37
Уравнение регрессии (эмпирическое уравнение регрессии):
y = e^0.37x^0.77 = 0,68x^0.77
Эмпирические коэффициенты регрессии a и b являются лишь оценками теоретических коэффициентов β_i, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных.

Коэффициент эластичности находится по формуле:

В нашем примере коэффициент эластичности больше 1. Следовательно, при изменении Х на 1%, Y изменится более чем на 1%. Другими словами - Х существенно влияет на Y.
Эмпирическое корреляционное отношение
Эмпирическое корреляционное отношение вычисляется для всех форм связи и служит для измерение тесноты зависимости. Изменяется в пределах [0;1].
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < η < 0.3: слабая;
0.3 < η < 0.5: умеренная;
0.5 < η < 0.7: заметная;
0.7 < η < 0.9: высокая;
0.9 < η < 1: весьма высокая;

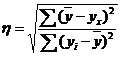
Индекс корреляции.
Величина индекса корреляции R находится в границах от 0 до 1. Чем ближе она к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии.

$Индекс корреляции: формула$

Полученная величина свидетельствует о том, что фактор x существенно влияет на y
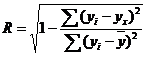
Для любой формы зависимости теснота связи определяется с помощью множественного коэффициента корреляции:

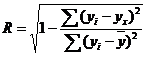
Данный коэффициент является универсальным, так как отражает тесноту связи и точность модели, а также может использоваться при любой форме связи переменных. При построении однофакторной корреляционной модели коэффициент множественной корреляции равен коэффициенту парной корреляции r_xy.
В отличие от линейного коэффициента корреляции он характеризует тесноту нелинейной связи и не характеризует ее направление. Изменяется в пределах [0;1].

Индекс детерминации.
Величину R² (равную отношению объясненной уравнением регрессии дисперсии результата у к общей дисперсии у) для нелинейных связей называют индексом детерминации.
Чаще всего, давая интерпретацию индекса детерминации, его выражают в процентах.

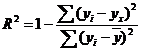
т.е. в 72.26 % случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - высокая. Остальные 27.74 % изменения Y объясняются факторами, не учтенными в модели.

ln(x)	ln(y)	x ²	y ²	x·y	y(x)	(y_i-y_cp) ²	(y-y(x))²
9.64	7.1	92.88	50.41	68.43	7.03	1.34	0.004311
11.2	8.95	125.36	80.03	100.16	8.23	0.47	0.51
13.7	10.15	187.73	102.99	139.05	10.16	3.57	0.000102
9.51	5.92	90.52	35.1	56.37	6.94	5.45	1.03
13.31	9.59	177.23	91.94	127.65	9.86	1.77	0.0735
12.35	7.52	152.63	56.49	92.86	9.12	0.55	2.58
9.43	7.11	89.01	50.62	67.13	6.88	1.31	0.0558
14.14	11.55	199.9	133.31	163.24	10.49	10.81	1.11
11.52	8.99	132.63	80.88	103.57	8.48	0.54	0.26
13.09	8.93	171.25	79.77	116.88	9.69	0.45	0.57
9.6	7.67	92.12	58.86	73.64	7	0.34	0.45
9.42	7.27	88.77	52.84	68.49	6.87	0.98	0.16
10.14	6.48	102.91	42.01	65.75	7.42	3.16	0.89
10.6	7	112.32	48.97	74.16	7.77	1.59	0.6
10.2	7.23	104.13	52.29	73.79	7.47	1.06	0.0572
13.42	10.74	180.21	115.36	144.18	9.95	6.16	0.63
12.35	9.21	152.62	84.81	113.77	9.12	0.9	0.007466
12.46	9.88	155.27	97.52	123.06	9.21	2.61	0.45
10.41	6.96	108.47	48.42	72.47	7.63	1.69	0.45
9.96	8.63	99.24	74.56	86.02	7.28	0.14	1.83
12.56	9.18	157.84	84.33	115.37	9.28	0.86	0.0101
11.68	8.73	136.51	76.23	102.01	8.61	0.22	0.0153
11.88	8.71	141.08	75.81	103.42	8.76	0.2	0.002472
10.42	6.31	108.65	39.77	65.74	7.64	3.81	1.78
10.27	6.69	105.47	44.8	68.74	7.52	2.45	0.68
12.06	9.52	145.53	90.72	114.9	8.9	1.6	0.39
7.41	6.47	54.93	41.89	47.97	5.32	3.19	1.32
11.67	8.74	136.1	76.45	102	8.59	0.24	0.0223
314.43	231.24	3601.3	1967.19	2650.8	231.24	57.47	15.94

Перейти к онлайн решению своей задачи

Индекс корреляции

Ввод данных

Правила ввода данных

Поиск

Процесс

Сообщение