Точки разрыва функции
Назначение
Сервис предназначен для определения типа точек разрыва функции.
Классификация точек разрыва
Для точек разрыва принята следующая классификация.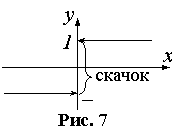
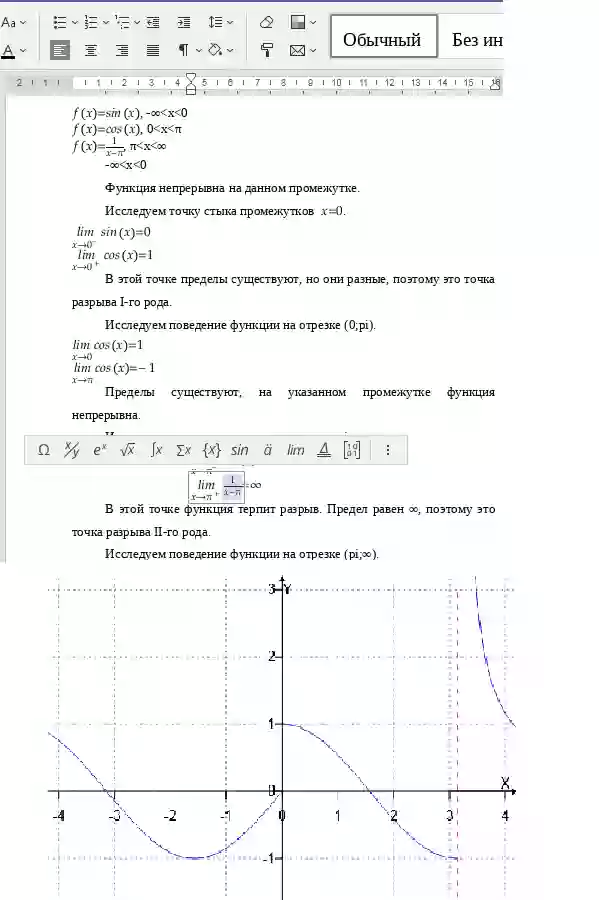
Если в точке имеются конечные пределы, но они не равны f(x0+0)≠f(x0-0), то x0 называется точкой разрыва первого рода, при этом разрыв называют скачком функции.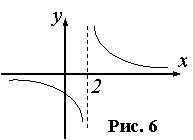
Точками разрыва второго рода называются точки, в которых хотя бы один из односторонних пределов равен ∞ или не существует.
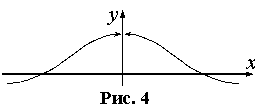Точка x=x0 называется точкой устранимого разрыва, если f(x0+0)=f(x0-0)≠f(x0). Разрыв «устраним» в том смысле, что достаточно изменить (доопределить или переопределить) функцию и функция станет непрерывной в точке x0.
Пример №1. Установить непрерывность или определить характер точек разрыва. Нарисовать график функции f(x) в окрестностях этих точек:
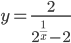
Решение. Найдем точки разрыва функции внутри указанной области.
Находим переделы в точке x=1.
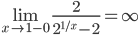
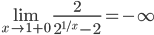
В этой точке функция терпит разрыв. Предел равен ∞, поэтому это точка разрыва II-го рода.
Находим переделы в точке x=0
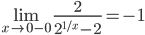
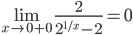
В этой точке функция терпит разрыв. Пределы существуют, но не равны, поэтому это точка разрыва I-го рода.
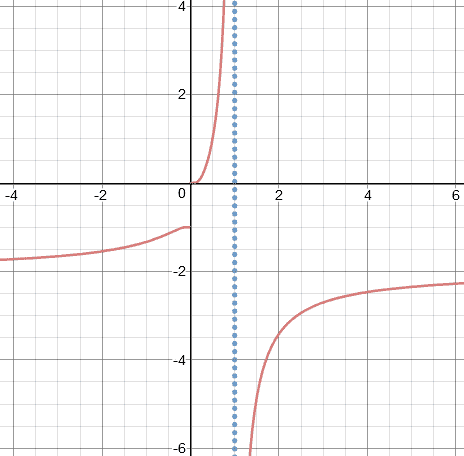
Ответ: точка x1=1 является точкой разрыва II-го рода, точка x2=0 является точкой разрыва I-го рода.
Пример №2. Найти точки разрыва функции, если они существуют. Сделать чертеж.
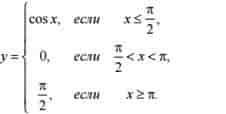
Решение. Исследуем точку стыка промежутков x=π/2
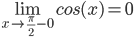
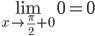
В этой точке пределы существуют и они равны, поэтому функция в этой точке непрерывна.
Исследуем поведение функции на отрезке (π/2;π).
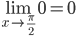
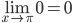
Пределы существуют, на указанном промежутке функция непрерывна.
Исследуем точку стыка промежутков x=π
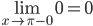
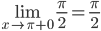
В этой точке пределы существуют, но они разные, поэтому это точка разрыва I-го рода.
Исследуем поведение функции на отрезке (pi;∞).
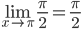
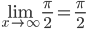
Пределы существуют, на указанном промежутке функция непрерывна.
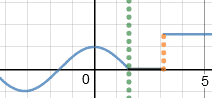
Ответ: Точка x=π является точкой разрыва I-го рода.
Пример №3. Найти точки разрыва функции и определить их тип.