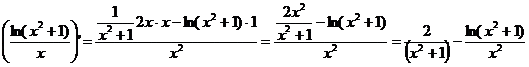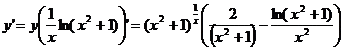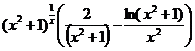Классификация точек разрыва функции
Непрерывность функции: основные понятия и свойства
Определение. Пусть на некотором промежутке определена функция f(x) и x0 – точка этого промежутка. Если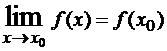 , то f(x) называется непрерывной в точке x0.
, то f(x) называется непрерывной в точке x0.
Из определения следует, что о непрерывности можно говорить лишь по отношению к тем точкам, в которых f(x) определена (при определении предела функции такого условия не ставилось). Для непрерывных функций
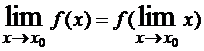 , то есть операции f и lim перестановочны. Соответственно двум определениям предела функции в точке можно дать два определения непрерывности – «на языке последовательностей» и «на языке неравенств» (на языке ε-δ). Предлагается это сделать самостоятельно.
, то есть операции f и lim перестановочны. Соответственно двум определениям предела функции в точке можно дать два определения непрерывности – «на языке последовательностей» и «на языке неравенств» (на языке ε-δ). Предлагается это сделать самостоятельно.
Для практического использования иногда более удобно определение непрерывности на языке приращений.
Величина Δx=x-x0 называется приращением аргумента, а Δy=f(x)-f(x0) – приращением функции при переходе из точки x0 в точку x.
Определение. Пусть f(x) определена в точке x0. Функция f(x) называется непрерывной в точке x0, если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции, то есть Δy→0 при Δx→0.
Пример №1. Доказать, что функция y=sinx непрерывна при любом значении x.
Решение. Пусть x0 – произвольная точка. Придавая ей приращение Δx, получим точку x=x0+Δx. Тогда Δy=f(x)-f(x0) = sin(x0+Δx)-sin(x) = 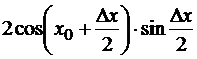 . Получаем
. Получаем 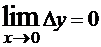 .
.
Определение. Функция y=f(x) называется непрерывной в точке x0 справа (слева), если
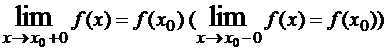
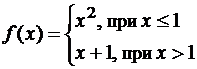
Определение. Функция называется непрерывной на некотором промежутке, если она непрерывна в каждой точке этого промежутка.
В частности, если промежутком является отрезок [a,b], то на его концах подразумевается односторонняя непрерывность.
Свойства непрерывных функций
1. Все элементарные функции непрерывны в своей области определения.2. Если f(x) и φ(x), заданные на некотором промежутке, непрерывны в точке x0 этого промежутка, то в этой точке будут также непрерывны функции
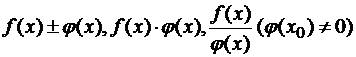
3. Если y=f(x) непрерывна в точке x0 из X, а z=φ(y) непрерывна в соответствующей точке y0=f(x0) из Y, то и сложная функция z=φ(f(x)) будет непрерывной в точке x0.
Разрывы функции и их классификация
Признаком непрерывности функции f(x) в точке x0 служит равенство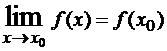 , которое подразумевает наличие трех условий:
, которое подразумевает наличие трех условий:
1) f(x) определена в точке x0;
2)
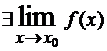 ;
;
3)
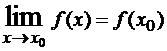 .
.
Если хотя бы одно из этих требований нарушено, то x0 называют точкой разрыва функции. Другими словами, точкой разрыва называется точка, в которой эта функция не является непрерывной. Из определения точек разрыва следует, что точками разрыва функции являются:
а) точки, принадлежащие области определения функции, в которых f(x) теряет свойство непрерывности,
б) точки, не принадлежащие области определения f(x), которые являются смежными точками двух промежутков области определения функции.
Например, для функции
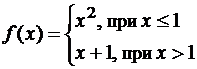 имеет разрыв в точке x=1, являющейся смежной для двух промежутков (-∞,1) и (1,∞) области определения f(x) и
имеет разрыв в точке x=1, являющейся смежной для двух промежутков (-∞,1) и (1,∞) области определения f(x) и Для точек разрыва принята следующая классификация.
1) Если в точке x0 имеются конечные 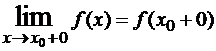 и
и 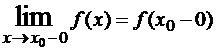 , но f(x0+0)≠f(x0-0), то x0 называется точкой разрыва первого рода, при этом
, но f(x0+0)≠f(x0-0), то x0 называется точкой разрыва первого рода, при этом ![]() называют скачком функции.
называют скачком функции.
Пример 2. Рассмотрим функцию 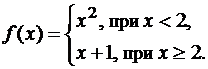
Разрыв функции возможен только в точке x=2 (в остальных точках она непрерывна как всякий многочлен).
 Найдем
Найдем ![]() ,
, ![]() . Так как односторонние пределы конечны, но не равны друг другу, то в точке x=2 функция имеет разрыв первого рода. Заметим, что
. Так как односторонние пределы конечны, но не равны друг другу, то в точке x=2 функция имеет разрыв первого рода. Заметим, что ![]() , следовательно функция в этой точке непрерывна справа (рис. 2).
, следовательно функция в этой точке непрерывна справа (рис. 2).
2) Точками разрыва второго рода называются точки, в которых хотя бы один из односторонних пределов равен ∞ или не существует.
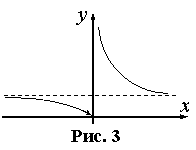 Пример 3. Функция y=21/x непрерывна для всех значений x, кроме x=0. Найдем односторонние пределы:
Пример 3. Функция y=21/x непрерывна для всех значений x, кроме x=0. Найдем односторонние пределы: ![]() ,
, ![]() , следовательно x=0 – точка разрыва второго рода (рис. 3).
, следовательно x=0 – точка разрыва второго рода (рис. 3).
3) Точка x=x0 называется точкой устранимого разрыва, если f(x0+0)=f(x0-0)≠f(x0).
Разрыв «устраним» в том смысле, что достаточно изменить (доопределить или переопределить) значение функции в этой точке, положив
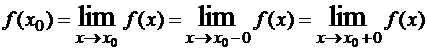
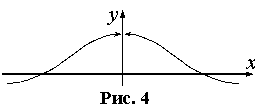 Пример 4. Известно, что
Пример 4. Известно, что 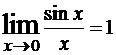 , причем этот предел не зависит от способа стремления x к нулю. Но функция
, причем этот предел не зависит от способа стремления x к нулю. Но функция 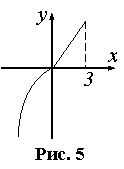 Пример 5. Исследовать на непрерывность функцию
Пример 5. Исследовать на непрерывность функцию 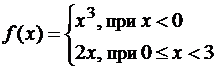 .
.
Решение. Функции y=x3 и y=2x определены и непрерывны всюду, в том числе и в указанных промежутках. Исследуем точку стыка промежутков x=0:
Определение. Функция, непрерывная на промежутке за исключением конечного числа точек разрыва первого рода или устранимого разрыва, называется кусочно-непрерывной на этом промежутке.
Примеры разрывных функций
 Пример 1. Функция
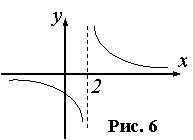
Пример 1. Функция 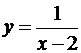 определена и непрерывна на (-∞,+∞) за исключением точки x=2. Определим тип разрыва. Поскольку
определена и непрерывна на (-∞,+∞) за исключением точки x=2. Определим тип разрыва. Поскольку 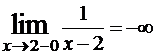 и
и 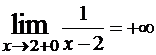 , то в точке x=2 разрыв второго рода (рис. 6).
, то в точке x=2 разрыв второго рода (рис. 6).
 Пример 2. Функция
Пример 2. Функция 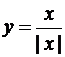 определена и непрерывна при всех x, кроме x=0, где знаменатель равен нулю. Найдем односторонние пределы в точке x=0:
определена и непрерывна при всех x, кроме x=0, где знаменатель равен нулю. Найдем односторонние пределы в точке x=0:
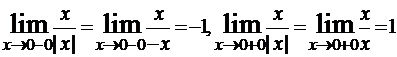 .
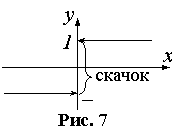
.Односторонние пределы конечны и различны, следовательно, x=0 – точка разрыва первого рода (рис. 7).
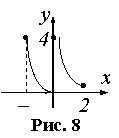 Пример 3. Установить, в каких точках и какого рода разрывы имеет функция
Пример 3. Установить, в каких точках и какого рода разрывы имеет функция 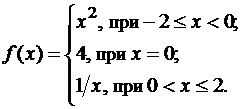
Эта функция определена на [-2,2]. Так как x2 и 1/x непрерывны соответственно в промежутках [-2,0] и [0,2], то разрыв может быть только на стыке промежутков, то есть в точке x=0. Поскольку
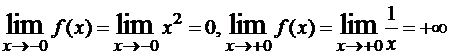
Пример 4. Можно ли устранить разрывы функций:
а) 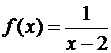 в точке x=2;
в точке x=2;
б) 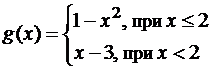 в точке x=2;
в точке x=2;
в) 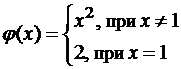 в точке x=1?
в точке x=1?
Решение. О примере а) сразу можно сказать, что разрыв f(x) в точке x=2 устранить невозможно, так как в этой точке бесконечные односторонние пределы (см. пример 1).
б) Функция g(x) хотя имеет конечные односторонние пределы в точке x=2
(![]() ,
,![]() ),
),
но они не совпадают, поэтому разрыв также устранить нельзя.
в) Функция φ(x) в точке разрыва x=1 имеет равные односторонние конечные пределы: ![]() . Следовательно, разрыв может быть устранен переопределением функции в точке x=1, если положить f(1)=1 вместо f(1)=2.
. Следовательно, разрыв может быть устранен переопределением функции в точке x=1, если положить f(1)=1 вместо f(1)=2.
Пример №5. Показать, что функция Дирихле
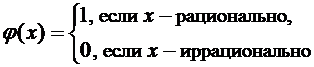
разрывна в каждой точке числовой оси.
Решение. Пусть x0 – любая точка из (-∞,+∞). В любой ее окрестности найдутся как рациональные, так и иррациональные точки. Значит, в любой окрестности x0 функция будет иметь значения, равные 0 и 1. В таком случае не может существовать предела функции в точке x0 ни слева, ни справа, значит функция Дирихле в каждой точке числовой оси имеет разрывы второго рода.
Пример 6. Найти точки разрыва функции
и определить их тип.Решение. Точками, подозрительными на разрыв, являются точки x1=2, x2=5, x3=3.
В точке x1=2 f(x) имеет разрыв второго рода, так как
Исследуем точку x3=3:
Для самостоятельного решения.
Исследовать функции на непрерывность и определить тип точек разрыва:
1) 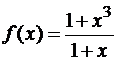 ; Ответ: x=-1 – точка устранимого разрыва;
; Ответ: x=-1 – точка устранимого разрыва;
2) 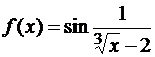 ; Ответ: Разрыв второго рода в точке x=8;
; Ответ: Разрыв второго рода в точке x=8;
3) 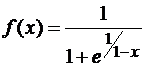 ; Ответ: Разрыв первого рода при x=1;
; Ответ: Разрыв первого рода при x=1;
4) 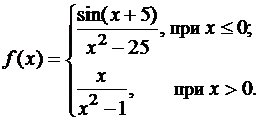
Ответ: В точке x1=-5 устранимый разрыв, в x2=1 – разрыв второго рода и в точке x3=0 - разрыв первого рода.
5) Как следует выбрать число A, чтобы функция
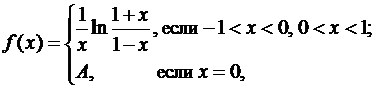
Ответ: A=2.
6) Можно ли подобрать число A так, чтобы функция
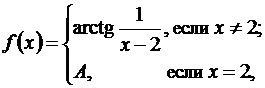
была бы непрерывной в точке x=2?
Ответ: нет.
Задана функция y=f(x) и два значения аргумента x1 и x2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной из данных значений аргумента; 2) в случае разрыва определить, какого он рода; 3) все рассуждения обосновать.
![]() , x1 = 1, x2 = 3
, x1 = 1, x2 = 3
Решение:
а) ![]()
Предел конечен и равен числу. Следовательно, в точке x1 функция непрерывна.
б) ![]()
![]()
Предел в точке x=3 не существует. Следовательно, в этой точке функция имеет разрыв. Поскольку один из пределов равен бесконечности, то эта точка разрыва второго рода.
в) ![]()
![]()
![]()