Первый замечательный предел
Соотношение вида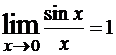 (или
(или 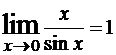 ) называют первым замечательным пределом. Дадим критерий для его распознавания:
) называют первым замечательным пределом. Дадим критерий для его распознавания:
1) выражение представляет собой неопределенность вида
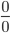 ,
,
2)
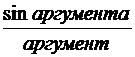 ,
,
3) аргумента → 0.
Найдем первый замечательный предел среди предложенных:
1)
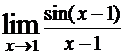 ; 2)
; 2) 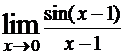 ; 3)
; 3) 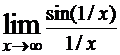 ;
;
4)
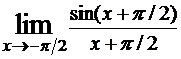 ; 5)
; 5) 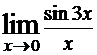 .
.
Пределы 1, 3 и 4 являются первыми замечательными, так как все три условия, перечисленные в критерии, выполнены. Во втором примере не выполнены первое и третье условия, поэтому это не есть первый замечательный предел (предел находится сразу в результате подстановки предельной точки). Пятый предел можно свести к первому замечательному, домножая числитель и знаменатель на 3.
При решении примеров следует иметь в виду, что предел выражения, содержащего любую тригонометрическую функцию и имеющего неопределенность вида
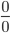 , всегда можно свести к первому замечательному пределу, однако в этом не всегда есть необходимость.
, всегда можно свести к первому замечательному пределу, однако в этом не всегда есть необходимость.
Примечание: число "пи" (π) записывается как pi, знак ∞ как infinity
Замечательные эквивалентности в пределах
ex-1 ≈ x, x → 0ln(1+x) ≈ x, x → 0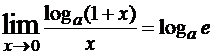

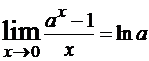
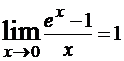
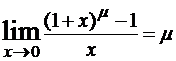
Примеры решений
Пример 1. Используя свойства бесконечно малых и бесконечно больших функций, найти следующие пределы:
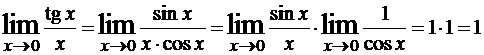 .
.
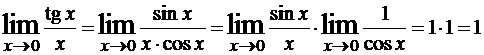 .
.
Пример 2.
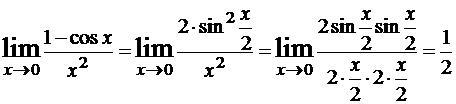 .
.
Пример 3.
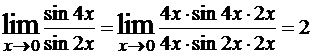 .
.
Пример 4.
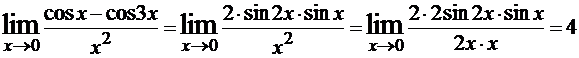 .
.
Пример 5.
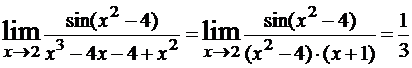 .
.
Пример 6.
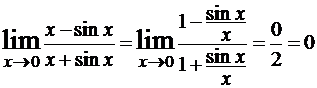 .
.
Пример 7.
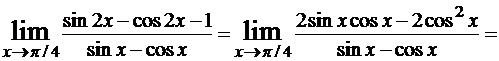
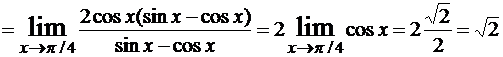 .
.
Пример 8. 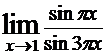 . Первый замечательный предел применить нельзя, так как аргументы πx и 3πx у синусов не стремятся к нулю при x=1. Поэтому положим x-1=y, тогда при x→1 будет y→0. Тогда
. Первый замечательный предел применить нельзя, так как аргументы πx и 3πx у синусов не стремятся к нулю при x=1. Поэтому положим x-1=y, тогда при x→1 будет y→0. Тогда
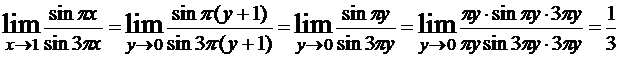 .
.
Пример 9. 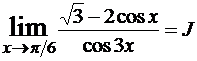 . Обозначим x-π/6=y, тогда
. Обозначим x-π/6=y, тогда
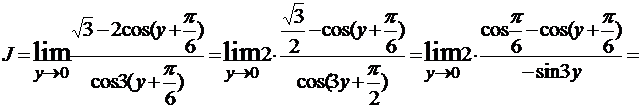
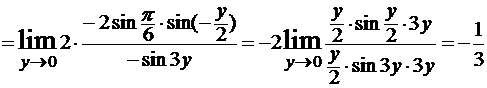 .
.
